命题逻辑中的条件关系

命题与条件的基本概念

命题

• 定义：是一个陈述句，这个句子具有明确的真值，即该陈述句要么是真的，要么是假的。通常用小写字母（如、）来表示简单命题。简单命题可以通过逻辑联结词组成复合命题。

例如：

雪是白色的。

• 这句话是陈述句
• 客观来说，该陈述句的描述是真的

条件

• 定义：条件特指命题之间的逻辑关系（如必要/充分条件），用于描述命题之间的蕴含性。
• 与命题的关系：
  • 必要/充分条件是通过命题之间的逻辑连接（如蕴含式）定义的；
  • 讨论条件时，必然涉及至少两个命题（如前提和结论）。

区别与联系

维度	命题	条件
基本单位	单个陈述	命题间的逻辑关系
真值属性	必为真或假	描述命题间的真值传递规则
数学表达
研究范畴	命题逻辑（Propositional Logic）	谓词逻辑（Predicate Logic）

命题间的逻辑关系

根据 libretexts.org 的分类，任何两命题的关系可归为四类：
1. 必要但非充分（如”男性”对”兄弟”）；
2. 充分但非必要（如”整除4”对”偶数”）；
3. 必要且充分（如”今日是7月4日”对”美国独立日”）；
4. 既不必要也不充分（如”面包涂花生酱”与”明天股市上涨”）。

充分条件

如果某个 命题成立，则必然导致另一个 命题的成立。我们称 命题是 命题的充分条件。

从命题间关系的角度来看

若：

则称 命题是 命题的充分条件。

从满足命题的对象集合之间的关系的角度来看

若：

那么满足的对象集合是满足的对象集合的子集，即：

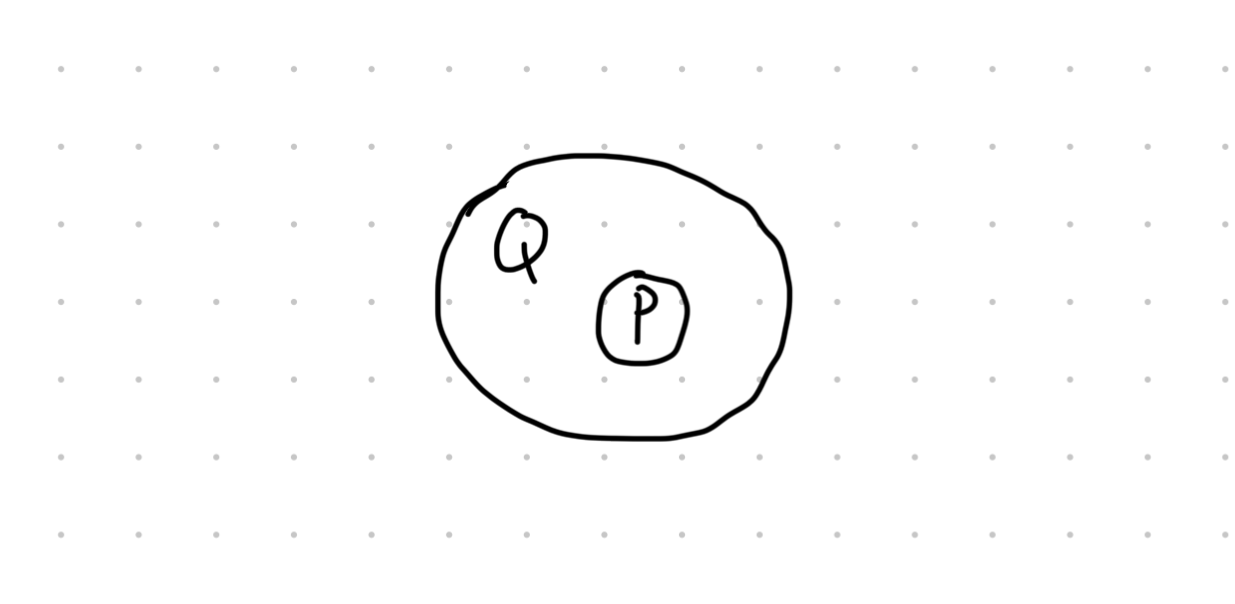
则称 命题是 命题的充分条件。

必要条件

如果某个 命题成立，则必然导致另一个 命题的成立。我们称 命题是 命题的必要条件。

从命题间关系的角度来看

若：

则称 命题是 命题的必要条件。

从满足命题的对象集合之间的关系的角度来看

若：

那么满足的对象集合是满足的对象集合的子集，即：

则称 命题是 命题的必要条件。

充要条件

如果某个 命题成立，则必然导致另一个 命题的成立，并且如果 命题成立，则必然导致命题的成立。那么我们称这两个条件互为充要条件。

从命题间关系的角度来看

若：

则称与互相为充要条件。

从满足命题的对象集合之间的关系的角度来看

若：

两个命题互为充要条件时，它们对应的对象集合完全相同：

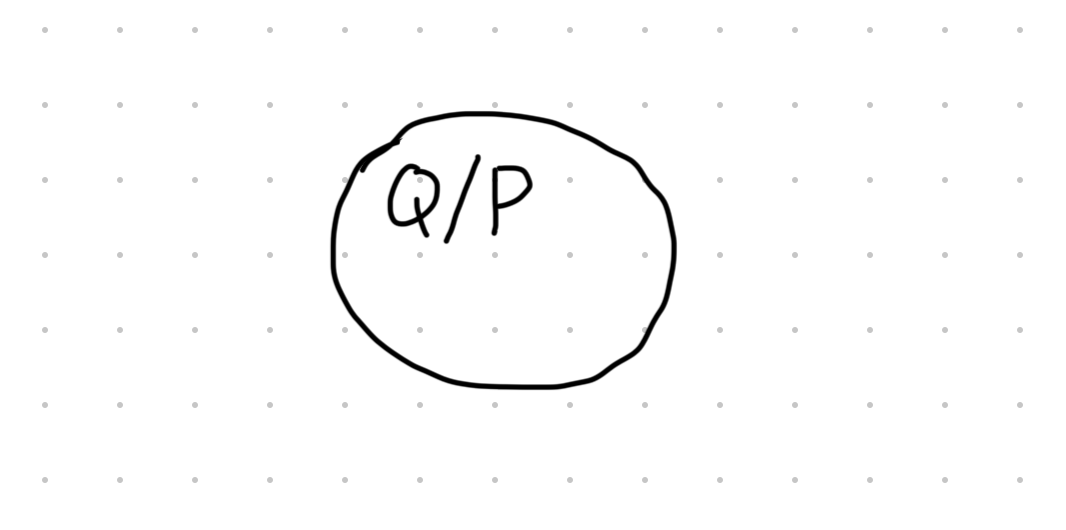
既非充分也非必要条件（无关条件）

当两个条件之间不存在任何逻辑蕴含关系时，两命题既非充分也非必要条件。

从命题间关系的角度来看

若：

则称：

• 既不是的充分或必要条件；
• 也不是的充分或必要条件。

从满足命题的对象集合之间的关系的角度来看

非包含

• （存在对象满足但不满足）
• （存在对象满足但不满足）

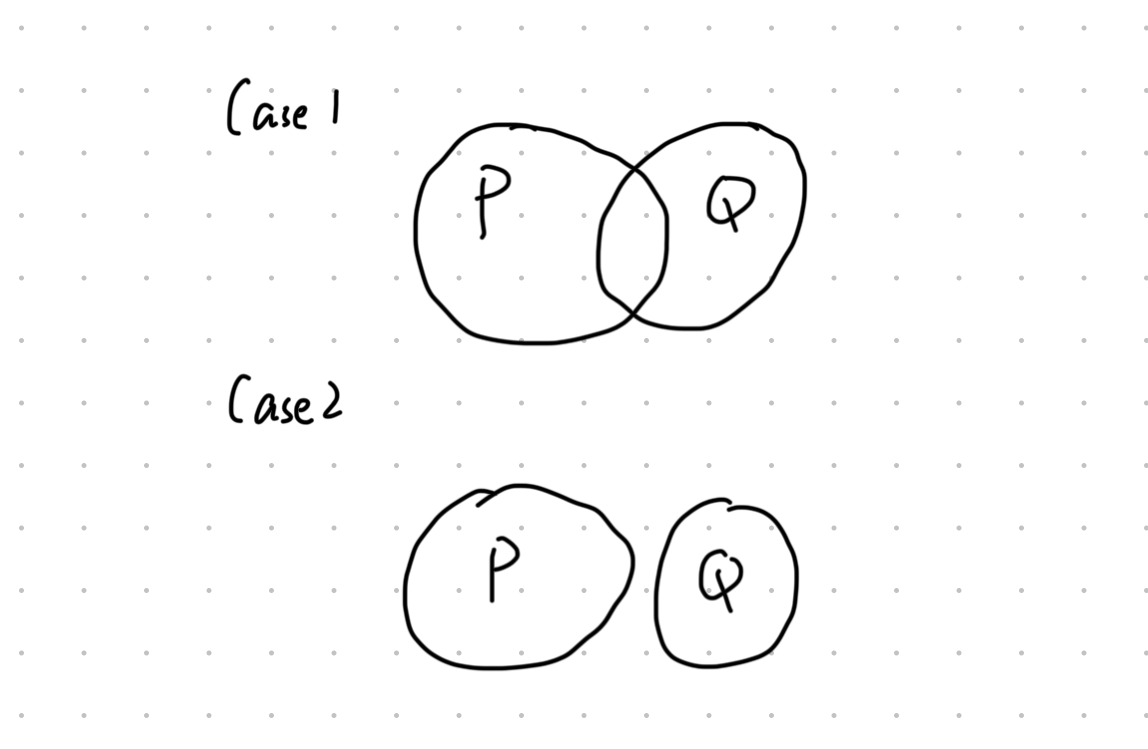
集合关系分类

• 部分交集：（存在同时满足和的对象）
• 完全独立：（无对象同时满足和）

逆否命题

若，则其逆否命题为
且 真值严格相同

证明

若，设全集为，定义满足命题的对象集合：

那么：

由图像容易看出：

又

则

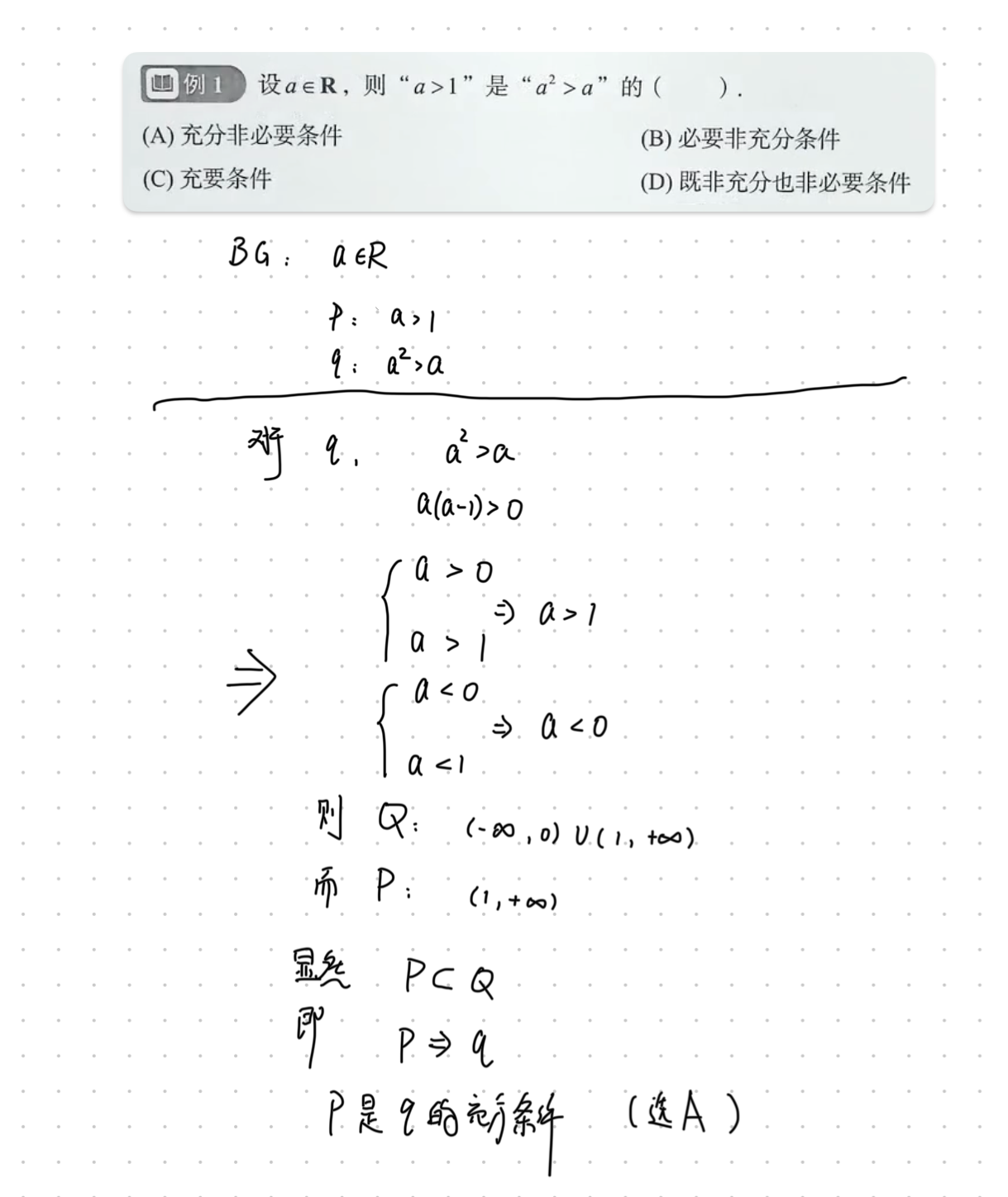
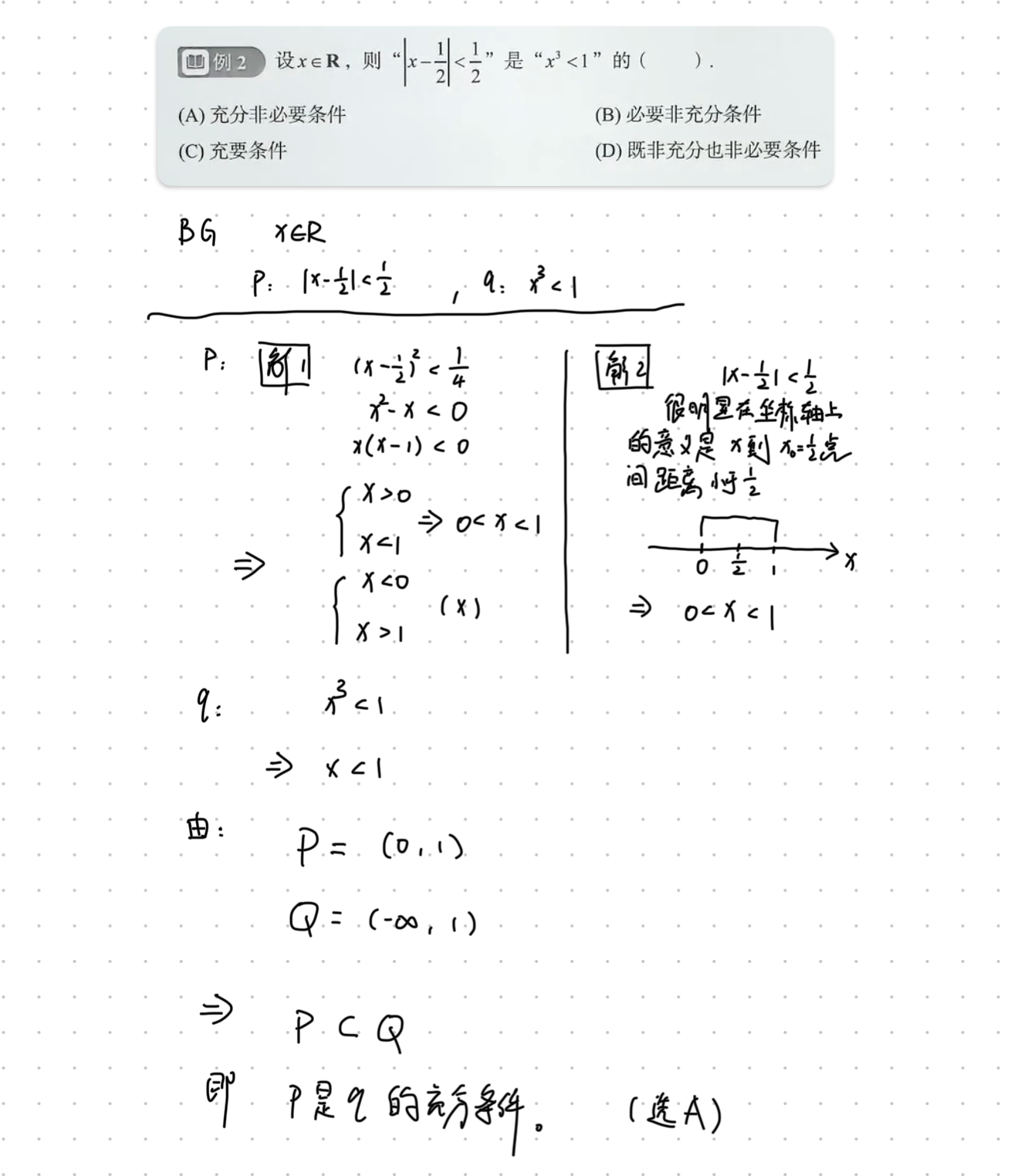
练习