
数学归纳法的学习与运用
数学归纳法简介
数学归纳法是一种严谨的数学证明方法,通过有限步骤验证无限个命题的有效性。其核心思想类似于多米诺骨牌效应:验证首张牌会倒下(基例),并证明任意一张倒下必定导致下一张倒下(归纳步骤),从而保证所有骨牌依次倾倒。
基本步骤
基例验证
首先验证命题在初始自然数(通常为
当
归纳假设
假设命题对某个自然数
归纳递推
证明命题对
这恰好对应
关键特征
严谨性:虽然名称含”归纳”,但实为演绎推理。通过有限步骤(基例验证+递推关系)保证所有自然数成立。
扩展形式:基例可从任意自然数
结构归纳:应用于递归定义的结构(如树、图),通过验证基本结构并保持递推性质完成证明。
练习

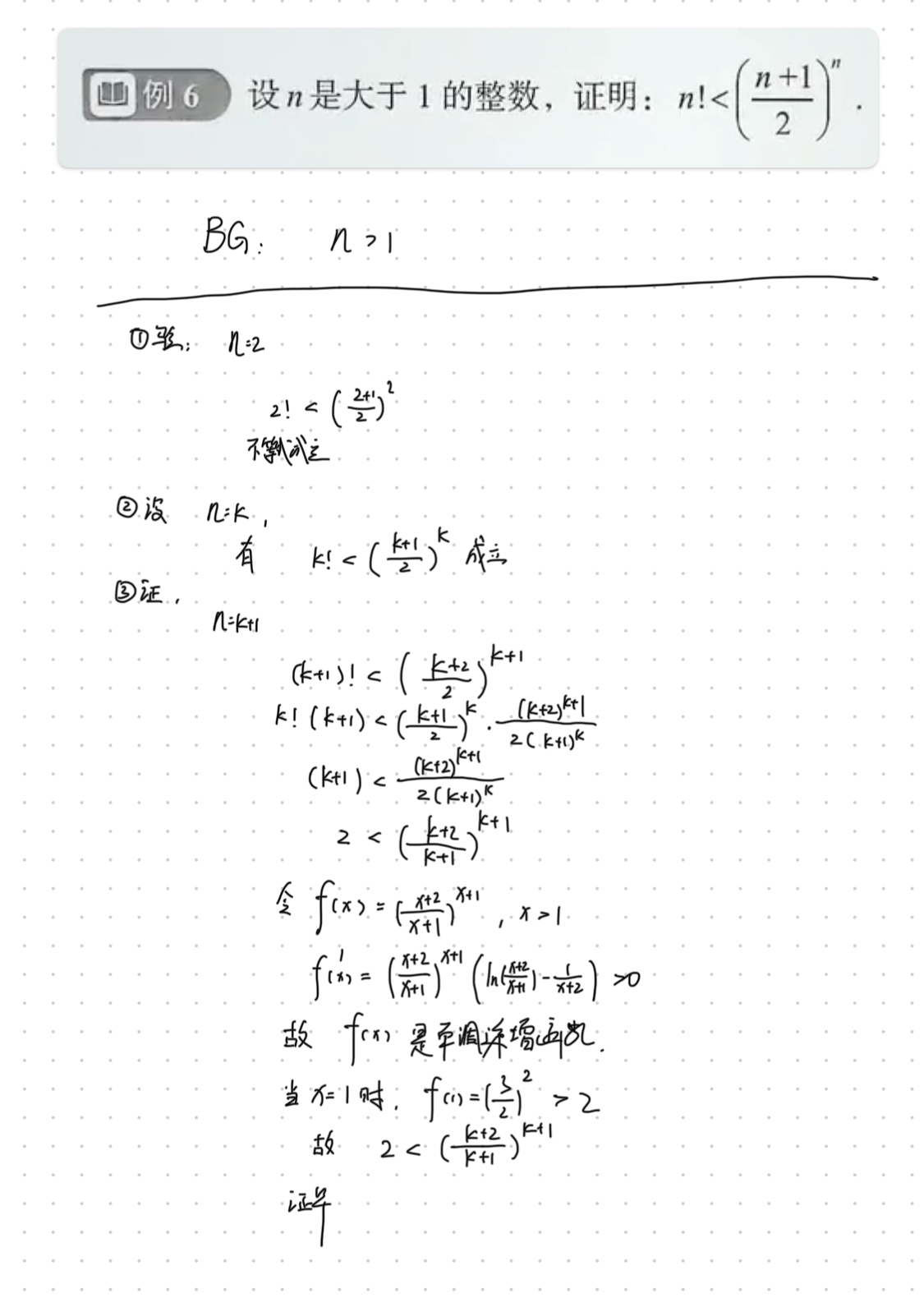

- Title: 数学归纳法的学习与运用
- Author: Neurocoda
- Created at : 2025-02-22 20:33:38
- Updated at : 2025-02-22 20:33:38
- Link: https://neurocoda.com/p/417b3d80.html
- License: This work is licensed under CC BY-ND 4.0.
Recommend
Recommend
Comments



