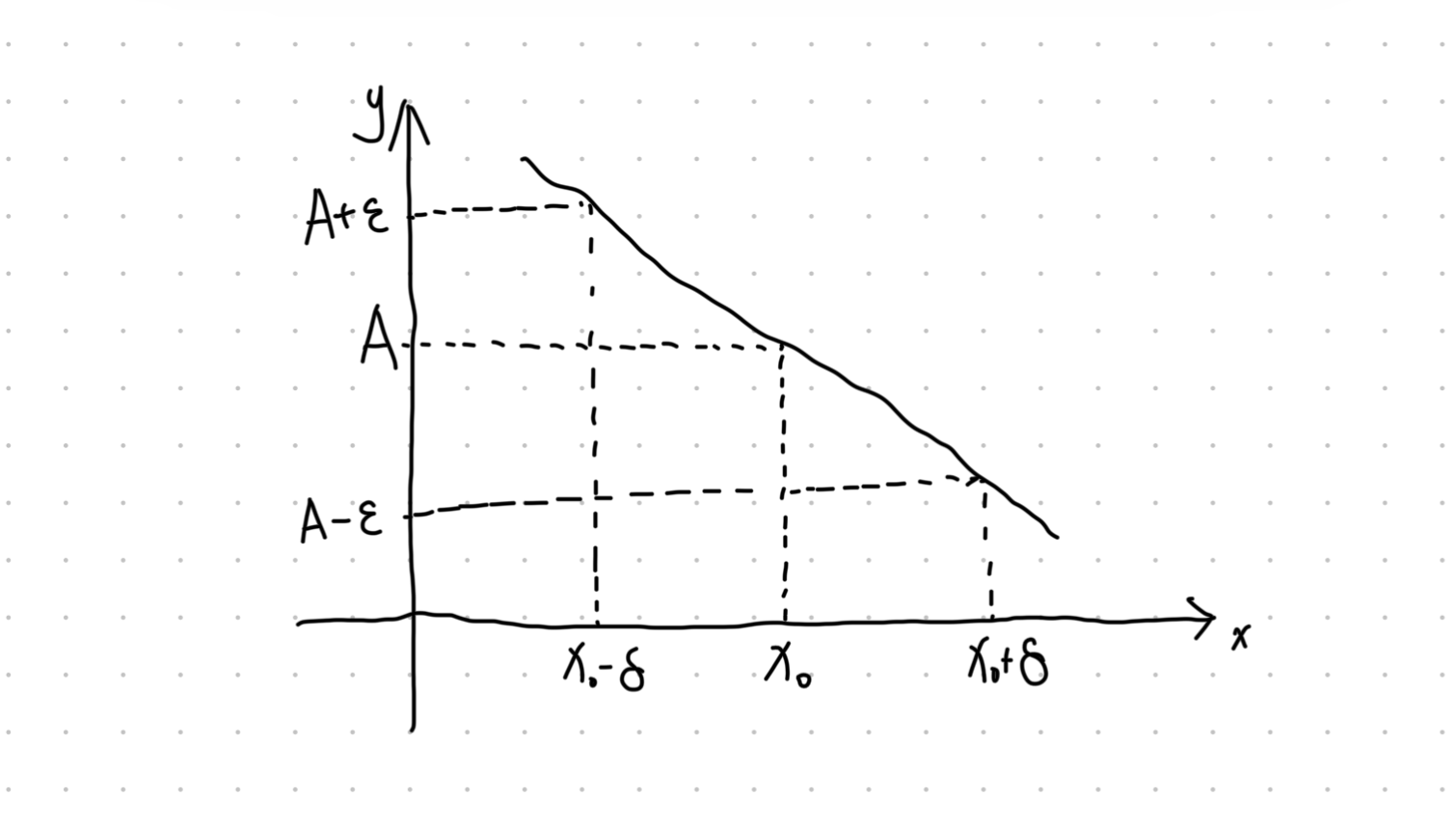
数系扩展梳理：以运算的不封闭性为线索

数学中的数系体系经历了从简单到复杂的扩展过程，由于实际需求及运算的不封闭性，出现了数学问题，因而出现了数系的扩展。

graph TD
    %% === 主干数系演进 ===
    A(自然数) -->|"减法不封闭"| B(整数)
    B -->|"除法不封闭"| C(有理数)
    C -->|"开方不封闭"| D(实数)
    D -->|"负数开方不封闭"| E(复数)

    %% 自然数对加法、乘法封闭
    A -.-> M[加法、乘法封闭]

    %% 整数子类
    B --> L[正整数、零、负整数]

    %% 有理数子类
    C --> F[分数形式]
    C --> G[有限小数]
    C --> H[无限循环小数]

    %% 实数子类
    D --> I[无理数]

    %% 复数子类
    E --> J[实数部分]
    E --> K[虚数部分]
    
    %% 样式定义（可选）
    classDef mainNode fill:#FCE7F3,stroke:#DB2777,stroke-width:2px,color:#831843
    classDef subNode fill:#FDF4FF,stroke:#9D174D,stroke-width:1px,color:#86198F
    classDef noteNode fill:#FFF7ED,stroke:#F97316,stroke-dasharray: 5 5,color:#C2410C

    %% 为具体节点分配样式
    class A,B,C,D,E mainNode
    class L,F,G,H,I,J,K subNode
    class M noteNode

• 自然数：对加、乘封闭，但减、除不封闭
• 整数：对加、减、乘封闭，但除法不封闭
• 有理数：对加、减、乘、除（除零外）封闭，但开方不封闭
• 实数：容纳无理数，能处理大部分根号运算（非负数开方），但负数开方仍无解
• 复数：引入，彻底解决负数开方的问题，对加减乘除等更高级运算也保持封闭

从“最初用来自然计数”的 自然数 出发，为了表达“少多少”或“亏多少”，我们纳入负数形成 整数；
再为了使“除法”有解，纳入分数形成 有理数；
之后为在数轴上容纳所有可能的无限小数，加入 无理数 形成 实数；
最后为了能处理负数开方，再添加 虚数单位形成 复数。

运算封闭性

运算的封闭性是代数系统中一个基础而重要的概念。它描述了一个集合在特定运算下是否保持结果的归属不变。具体来说，如果对集合中的元素进行某种运算后，结果仍然属于原集合，则称该集合对这种运算具有封闭性。

数学定义

设是一个非空集合，是定义在上的二元运算。若满足：

则称集合对运算封闭。反之，则称该运算不封闭。

自然数

包含哪些数？
通常指

有时也包含，写作。无论是否含，自然数都不出现负数或小数。

典型子类 / 记号

• 若包含：常用或
• 若不含：直接写

运算及封闭性

• 加法、乘法 封闭
  • 例：仍在，也在
• 减法、除法 不封闭
  • 例：不在，也不在

由于无法在自然数里表达“少几件”、“欠几元”或“半块蛋糕”的情况，我们引入了 负数（以及零），形成了 整数。

整数

包含哪些数？

把自然数的正部分、零、负数全部纳入，方便处理关于“多少超出/不足”的问题。

典型子类 / 记号

• 正整数：
• 负整数：
• 零：

运算及封闭性

• 加法、减法、乘法 封闭
  • 例：，，都是整数
• 除法 不封闭
  • 例：并不在

由于整数对除法仍不封闭（无法表示等分数），我们继续引入 分数，扩展到 有理数。

有理数

包含哪些数？

所有能写成分数形式的数，即分子分母均为整数、分母不为零。

典型形式 / 子类

• 分数形式：如、、
• 有限小数：如（可视作、）
• 无限循环小数：如、

运算及封闭性

• 加、减、乘、除（除数不为） 封闭
• 开方 不封闭
  • 例：并不属于任何分数，故不在之内

于是，为了在数轴上容纳等“无理数”，人们又扩展到 实数，并填满了数轴。

实数

包含哪些数？

把所有有理数和 无理数（小数形式为无限不循环）合并起来，也就把数轴上所有点全部“占满”。

典型子类 / 记号

• 无理数：如、、、
• 有理数：前面提到的分数及其等价小数形式

运算及封闭性

• 加、减、乘、除（除数不为） 封闭
• 开方（对非负数） 封闭
  • 例：等都在
• 负数的偶次根（如）仍不在实数范围

于是，为处理诸如的问题，我们引入 虚数，进入 复数 的领域。

复数

包含哪些数？

在这里，称为实部，称为虚部。若，就退化为纯实数；若且，则是纯虚数。

运算及封闭性

• 加减乘除 均封闭
  • 例：
  • 例：
• 负数开方：得以在复数范围内存在
  • 例：，等

复数在高等数学、物理和工程中非常重要，比如电路分析中的阻抗常写作（工程中用表示），就是典型的复数应用。

在更高层面上，还有四元数、超复数、超实数以及各种抽象代数结构，但其思想本质并未脱离“让原本不封闭的运算能有处安放”的出发点。正是这条 “需求驱动” 的主线，让数的家族从最初的自然数，不断演进至今天丰富多彩的数学世界。