解析式的分类及部分运算:自下而上方法
解析式 是用数学公式明确表达变量之间关系的方式,常见于函数、几何图形等数学对象的定义。
概念结构如下:
flowchart TD
解析式 --> 代数式
解析式 --> 超越式
代数式 --> 有理式
代数式 --> 无理式
有理式 --> 整式
有理式 --> 分式
整式 --> 单项式
整式 --> 多项式单项式
单项式 是由数字与变量的积组成的式子,其中数字叫 系数,变量的指数叫 次数,其中变量的指数必须为非负整数。例如
单项式的特征
- 系数:单项式中的数字因子。例如在
中,系数为 。 - 变量:表达式中的字母部分。如
包含变量 和 。 - 次数(度):所有变量指数的总和。例如:
的次数为 - 常数项
的次数为
| 单项式示例 | 系数 | 变量 | 次数 |
|---|---|---|---|
| 6 | x,y | 3 | |
| -1 | p | 4 | |
| π | r | 2 |
单项式的运算
加、减法
仅同类项(相同变量及指数)可相加减
无法合并
乘法
系数相乘,变量指数相加:
除法
系数相除,变量指数相减:
多项式
多项式 是由多个 单项式 通过加减法构成的代数式,其中 次数最高的单项式次数 称为该多项式的次数,所含 不同变量种类数 称为元,单项式的个数 称为项数。例如
多项式的特征
- 项数:组成多项式的单项式数量
- 次数:各单项式次数中的最大值
- 元数:表达式中不同字母变量的种类数
| 多项式示例 | 次数 | 项数 | 元数 |
|---|---|---|---|
| 3 | 3 | 1 | |
| 2 | 2 | 2 | |
| 4 | 1 | 1 |
多项式的运算
加、减法
合并同类项(变量及指数相同的项)
乘法
运用分配律逐项相乘:
特殊乘法公式
平方差公式:
- 应用示例:
- 应用示例:
完全平方公式:
- 应用示例:
- 拓展:二项式定理
- 应用示例:
整式
单项式 和 多项式 统称为 整式。
分式
分式 是用
且当 分子 的次数小于 分母 的次数时,称为 真分式;否则称 假分式。
分式的组成
- 分子:分式横线以上的整式
- 分母:分式横线以下的整式
| 分式示例 | 分子 | 分母 | 限制条件 |
|---|---|---|---|
分式的基本性质
分式的分子和分母同时乘以或除以同一个 非零整式,分式的值不变:
应用场景:
- 约分:消去分子分母的公因式
- 通分:化为同分母分式
分式的运算
加减法
同分母:直接加减分子
异分母:通分后加减
- 示例 1:同分母
- 示例 2:异分母
乘除法
乘法:分子乘分子,分母乘分母
除法:转化为乘倒数
- 乘法示例:
- 除法示例:
有理式
整式 和 分式 统称为 有理式。
有理式的计算(补充)
整式乘法
满足两种特殊条件则可以使用 系数竖式计算法;所有情况下都可以使用 竖式计算法。
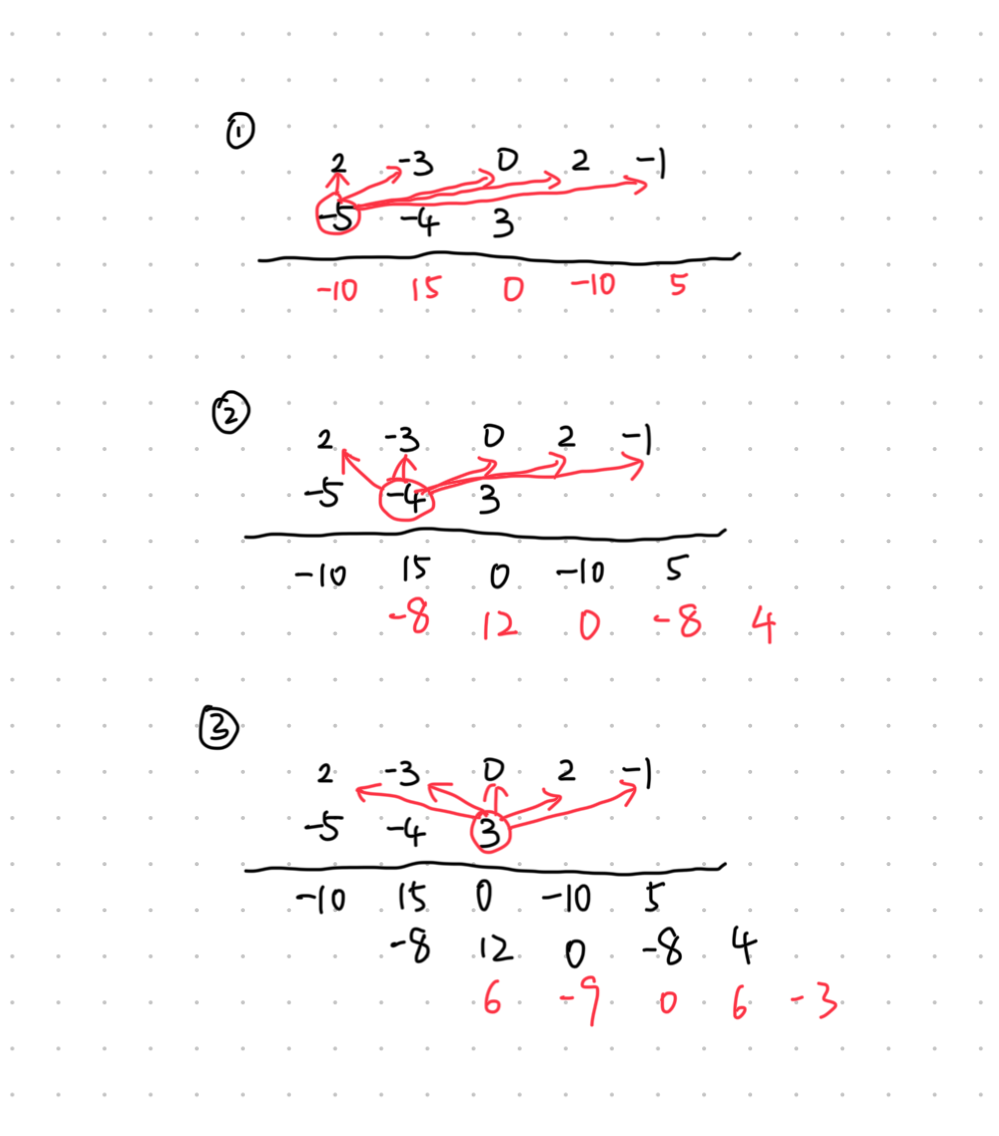
系数竖式计算法
BG:当
, 为整式,且均只含同一字母。
假设:
- 将
, 系数按降次排列,缺项补 ,写成两行,项多的写在第一行: 
- 竖式相乘,第二行每个系数乘以第一行每个系数,乘积结果对应排列:

- 竖式相加:
 得到:
得到:
BG:当
, 为整式,且均只含两个相同的字母。且可按某一字母降次、另一字母升次排列
假设:
将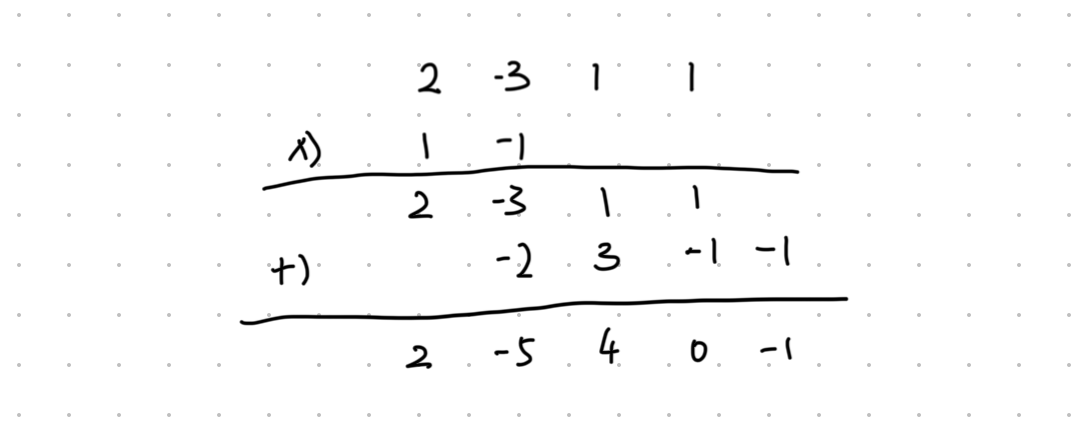
得到:
竖式计算法
BG:所有情况都适用
假设:
则:
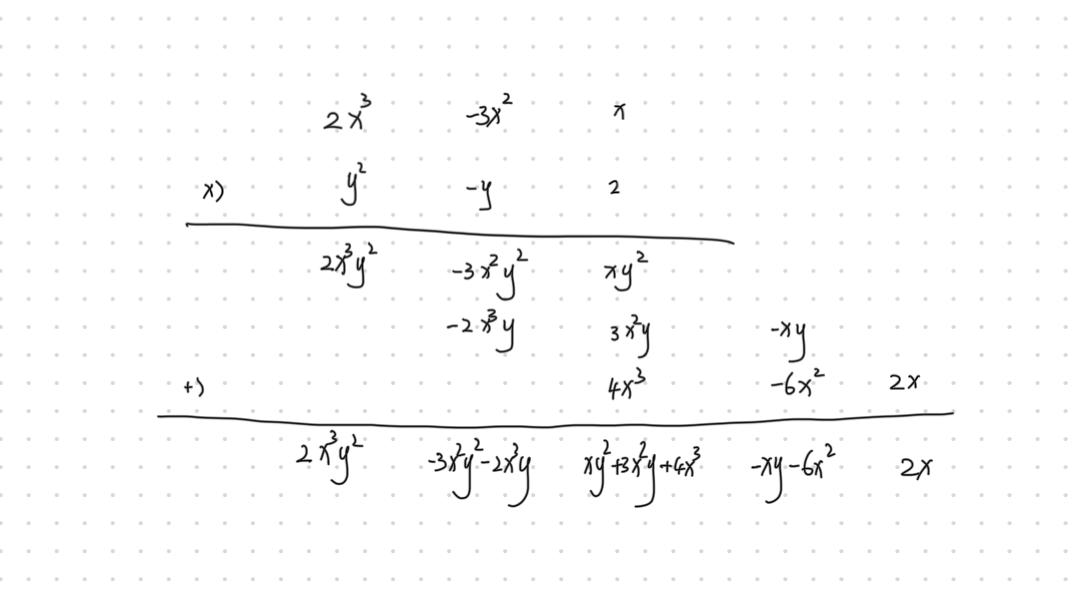
得到:
分式运算
化简有理分式
多项式长除法
BG: 先将被除式与除式作因式分解(如果可以的话)
假设:
则:

无理式
无理式 是代数式中包含 变量在根号内 的表达式,且根指数为 正整数。例如
无理式的组成
- 根指数:根号的左上角数字(默认二次根式不标注)
- 被开方式:根号内的代数式
| 无理式示例 | 被开方式 | 变量取值范围 |
|---|---|---|
| 全体实数 | ||
| 全体实数 | ||
无理式的基本性质
根式化简:
示例:, 运算性质:
- 乘方与开方互为逆运算:
- 同次根式相乘:
- 乘方与开方互为逆运算:
无理式的运算
加减法
同类根式(根指数与根号内代数式均相同)才可合并
- 示例 1:同类根式
- 示例 2:非同类根式
乘除法
同次根式:直接应用根式运算法则
异次根式:先统一根指数再运算
- 乘法示例:
- 除法示例:
有理化
消除分母中的根号
- 单根式有理化:
- 双根式有理化(平方差法):
注意事项
- 定义域优先:运算前需明确变量取值范围,例如
要求 。 - 最简形式:结果需满足:
- 根号内不含分母
- 根号内无平方因子(如
)
- 复合运算顺序:先化简再运算。
代数式
有理式 和 无理式 统称为 代数式。
超越式
超越式 是包含 非代数运算 的表达式,主要包括的运算有:
- 指数运算(变量位于指数位置,如
) - 对数运算(如
) - 三角函数(如
) - 反三角函数(如
)
这类式子无法通过有限次代数运算(加、减、乘、除、开方)转化为多项式或分式形式。
超越式的组成
| 类型 | 关键元素 | 示例 | 限制条件 |
|---|---|---|---|
| 指数型 | 底数、指数变量 | 底数 | |
| 对数型 | 底数、真数变量 | 真数 | |
| 三角型 | 角度变量、三角函数符号 | ||
| 反三角型 | 变量、反三角函数符号 |
超越式的基本性质
不可代数化简性:
超越式一般无法通过代数操作消除非代数运算符号。- 例如:
无法简化为多项式
- 例如:
运算封闭性:
超越式之间的组合通常仍为超越式(如)。 特殊运算规则:
- 指数律:
- 对数律:
- 三角恒等式:
- 指数律:
超越式的运算
加减法
一般无法合并简化,需保留原式
- 示例:
乘除法
部分类型可通过公式转化
- 指数型相乘:
- 对数型相除:
复合运算
嵌套超越函数需注意定义域
- 示例:
解析式
代数式和超越式统称为解析式。
- Title: 解析式的分类及部分运算:自下而上方法
- Author: Neurocoda
- Created at : 2025-02-23 19:32:06
- Updated at : 2025-02-23 19:32:06
- Link: https://neurocoda.com/p/6f246e82.html
- License: This work is licensed under CC BY-ND 4.0.

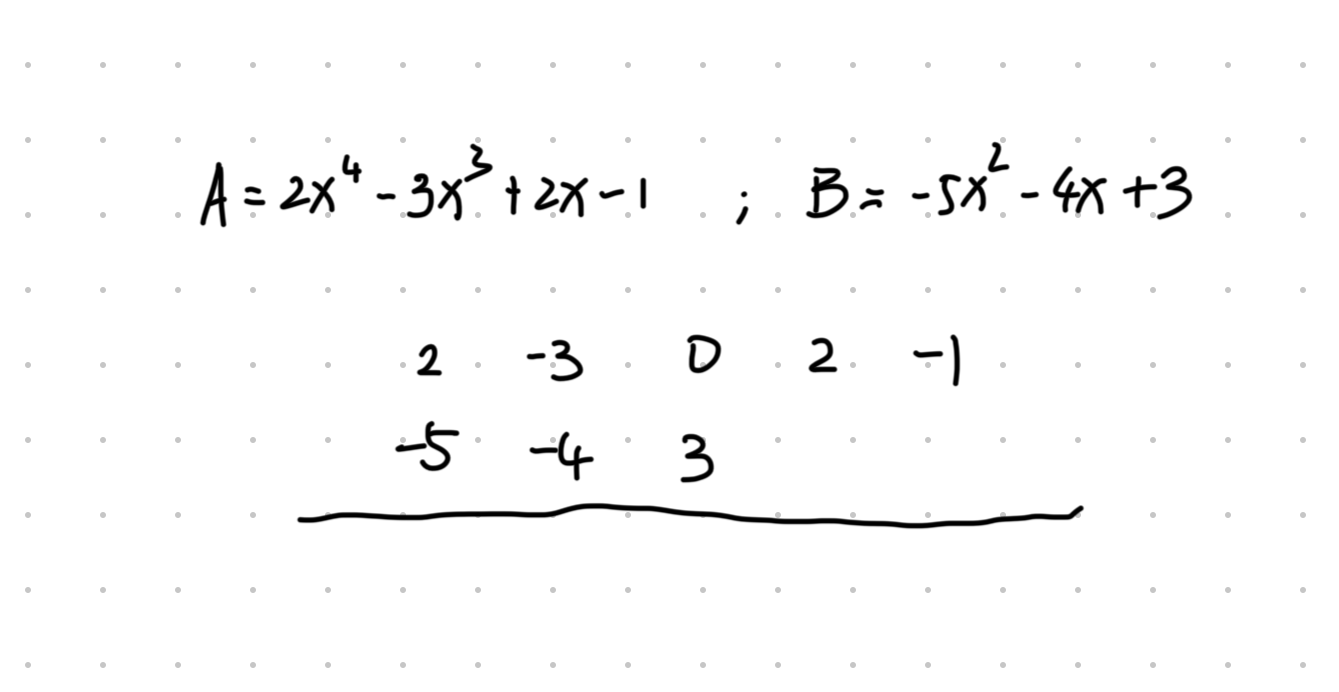
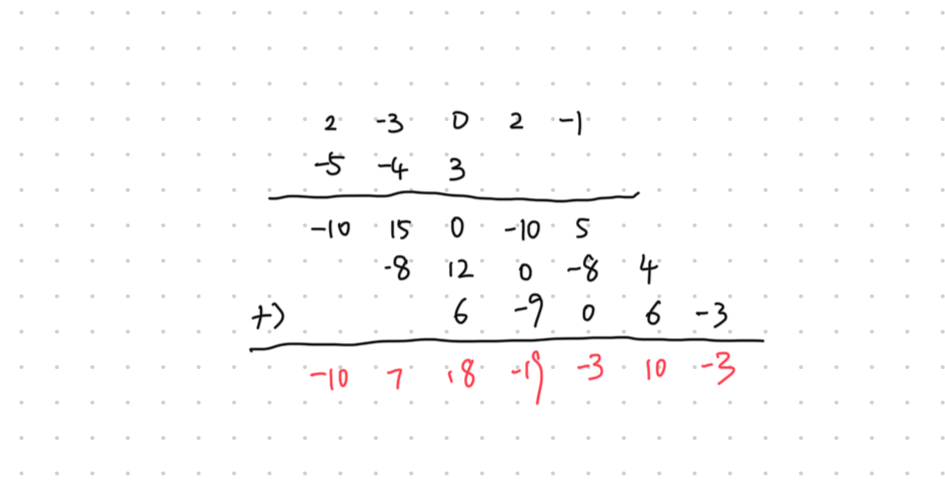 得到:
得到: