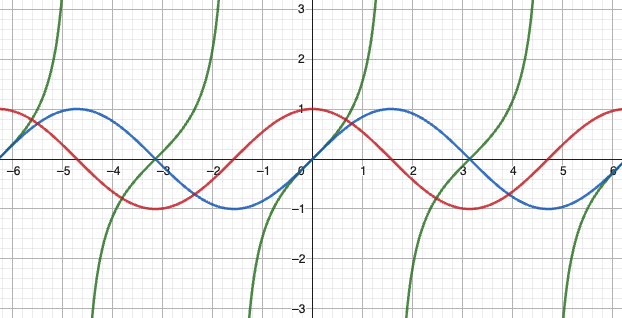
函数周期性的判断

要准确判断函数周期性需要系统分析函数结构并结合数学定义。我们首先从基础定义出发，再深入探讨复合函数情形，最后通过典型例题加深理解。

基本定义与判定方法

函数满足存在 非零实数使得对于定义域内所有都有：

则称为周期函数，最小的正周期称为 基本周期。

基本判定步骤：

1. 观察函数类型：三角函数（如、）、常数函数等具有明确周期性
2. 验证定义关系式：通过解方程寻找可能的周期
3. 确定最小正周期：验证候选周期中最小正数

示例：
满足：

故基本周期为

复合函数周期性分析

函数叠加

设周期为，周期为，当两周期比为有理数时，叠加函数 可能 存在周期：

判定条件：

1. 计算周期比（为互质整数）
2. 叠加函数的可能周期为

示例 2：
（）与（）叠加：

叠加函数周期为

函数复合

设外函数周期为，内函数周期为，复合函数的周期性需满足：

且需满足外函数周期关系：

示例 3：
分析的周期性：

• 内函数周期为
• 外函数周期为
• 复合函数满足，取最小正整数，故复合函数周期为

特殊情形处理

不同周期无公倍数

当周期比为无理数时，叠加函数不具有周期性。如：

由于为无理数，故叠加函数无周期

动态调整周期

当复合结构包含线性项时，需要重新推导周期性。例如：

虽然周期为，但复合后的函数周期需要通过方程验证：

要求是的整数倍且是的整数倍，最小周期为

组合导致非周期性情形

周期比无理数的叠加组合

当两个周期函数的周期比为无理数时，其线性组合将失去周期性

示例：

• 周期
• 周期
• 周期比（无理数）
• 叠加函数无周期性

周期函数与非周期函数复合

当周期函数与非周期函数进行函数复合时，通常会破坏周期性

典型组合：
其中为非周期函数
示例：

• 内函数是严格单调函数
• 无法找到使得
• 复合结果无周期性

多项式型叠加

周期函数与多项式函数叠加时，多项式项的持续增长会破坏周期性

示例：

• 当时，0.1x 项使函数值持续增长
• 无法满足
• 函数整体失去周期性

指数型调制

周期函数与指数函数相乘时，指数项的单调性会覆盖周期性

示例：

• 振幅呈指数衰减
• 虽然局部呈现波动，但整体不满足周期定义
• 当时振幅趋于零，无法保持周期性

特殊组合情形

周期函数与随机过程组合

周期函数与随机信号叠加会产生非周期结果

示例：

其中是白噪声

• 随机扰动破坏精确的周期性
• 严格数学意义上失去周期性

分数阶周期组合

当组合涉及非整数阶周期变换时可能破坏周期性

示例：

• 周期
• 周期
• 周期比为无理数
• 叠加后无周期性

重要结论总结

1. 叠加函数周期需两周期之比为有理数
2. 复合函数周期与内函数周期密切相关
3. 周期函数经过线性变换后，新周期为
4. 绝对值运算可能改变周期性特征
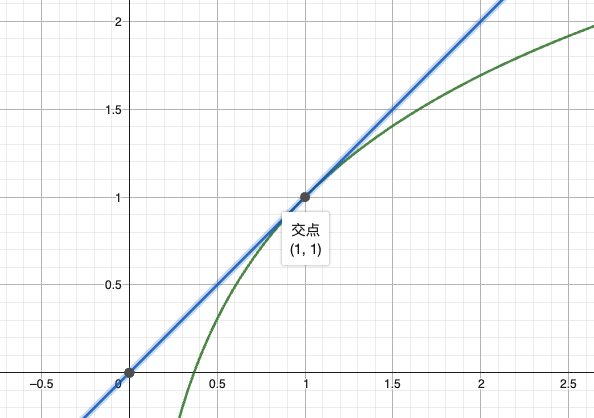
5. 非周期函数的复合可能产生周期性（如无周期性）

保持周期性的本质要求是所有组成元素的振动模式能形成共振，当存在不可调和的频率差异或单向趋势分量时，整体周期性就会被破坏。

练习
判断的周期性：

• 周期
• 周期
• 周期比（无理数）
• 结论：该叠加函数无周期性