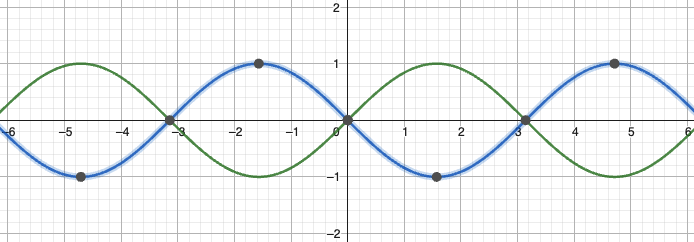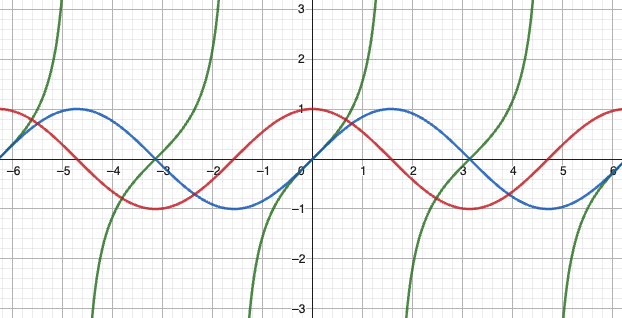
三角函数的图像与特性
三角函数
标准形式

基本特性
正弦函数
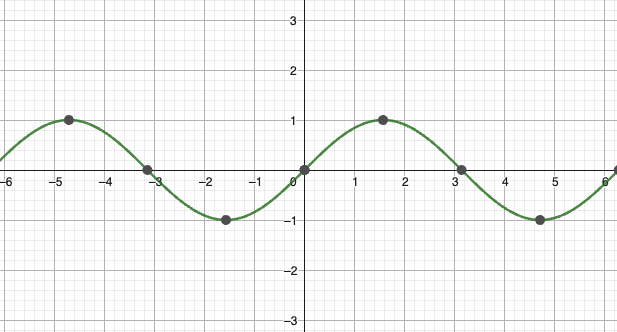
- 周期:
- 对称性:奇函数
- 极值点:
- 零点:
余弦函数
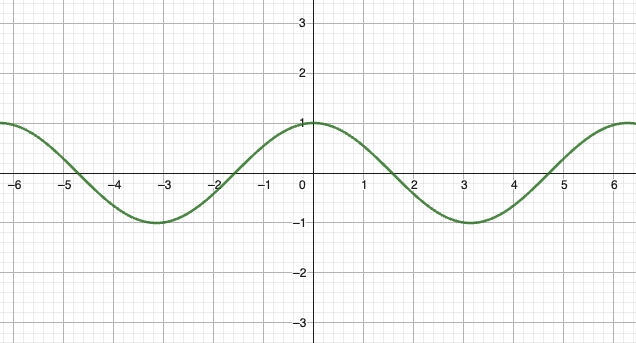
- 周期:
- 对称性:偶函数
- 极值点:
- 零点:
正切函数
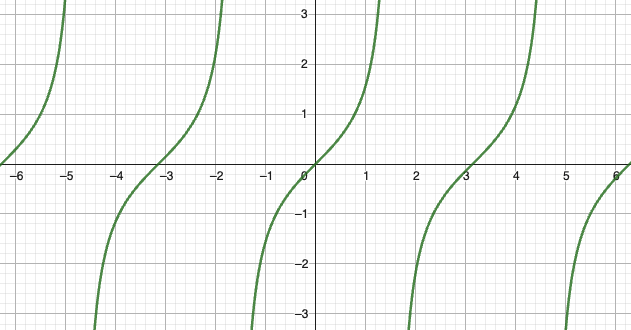
- 周期:
- 渐近线:
- 值域:
- 特殊点:过原点,周期中心对称
核心性质
导数与积分
| 函数 | 导数 | 积分 |
|---|---|---|
重要恒等式
毕达哥拉斯恒等:
和角公式:
函数对比分析
| 特性 | 正弦函数 | 余弦函数 | 正切函数 |
|---|---|---|---|
| 初始值 | 0 | 1 | 0 |
| 极值点 | 奇数次 | 偶数次 | 无 |
| 周期性 | |||
| 渐近线 | 无 | 无 | 存在 |
诱导公式
简述
- 拆分角度:将目标角表示为
- 判断奇偶:确定
- 象限定位:确定
- 综合结果:将符号与函数名组合得到最终表达式
核心原理解析
奇变偶不变:函数名的变换规律
当角度为
- 奇变:若
- 偶不变:若
示例分析:
符号看象限:函数值的符号判定
假设
象限符号口诀:
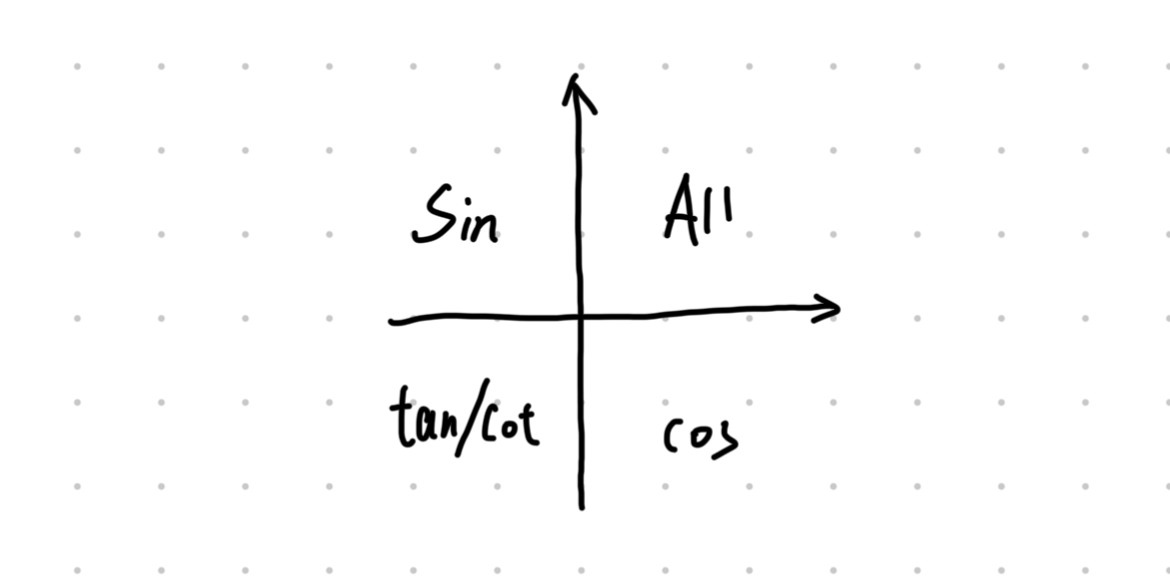
一全正,二正弦,三双切,四余弦
判定步骤:
- 确定
- 根据象限判断新函数的符号
- 将符号赋予化简后的结果
示例解析:
- 偶不变
- 第三象限余弦为负
- 结果为
- 奇变
- 第三象限正弦为负
- 结果为
综合应用示例
例1:化简
- 拆分角度:
- 函数名变换:
- 象限判定:
- 结果:
推导过程:
例2:计算
- 拆分角度:
- 函数名变换:
- 象限判定:
- 结果:
公式推导:
特殊情形处理
角度超出
- 先对角度取模
负角度的处理:
- 利用奇偶性转换。例如
反三角函数
标准形式
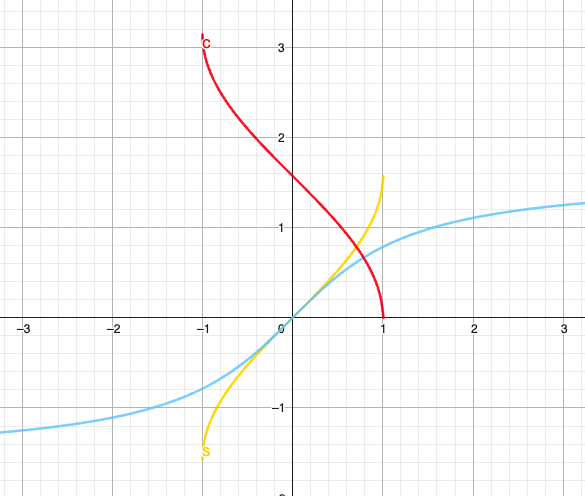
| 函数 | 定义域 | 值域 | 单调性 |
|---|---|---|---|
| 严格增 | |||
| 严格减 | |||
| 严格增 |
基本函数特性
反正弦函数
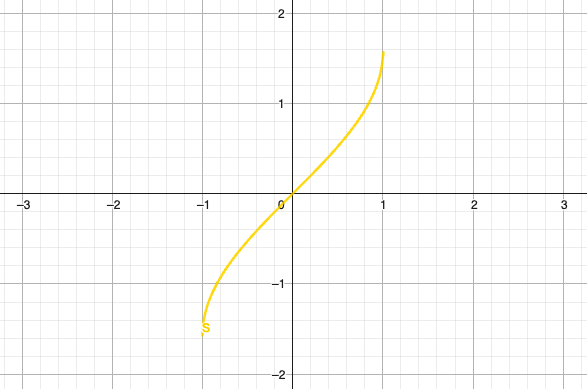
- 定义域:
- 值域:
- 导数:
- 单调性:严格单调递增
- 特殊值:
反余弦函数
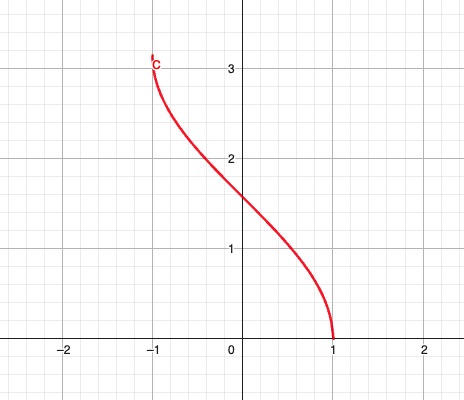
- 定义域:
- 值域:
- 导数:
- 单调性:严格单调递减
- 恒等式:
反正切函数
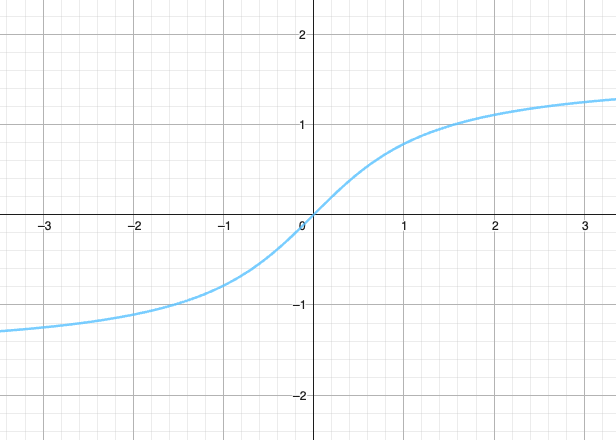
- 定义域:
- 值域:
- 导数:
- 渐近线:
- 对称性:
典型应用:
当
积分公式:
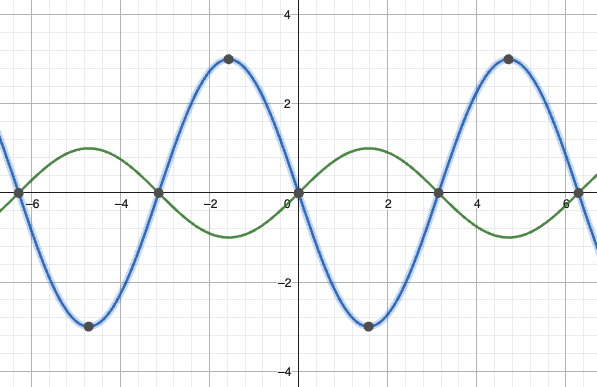
图像与参数的影响
以
基本参数
振幅调制:
频率变化:
相位移动:
复合波形示例:
图像变换
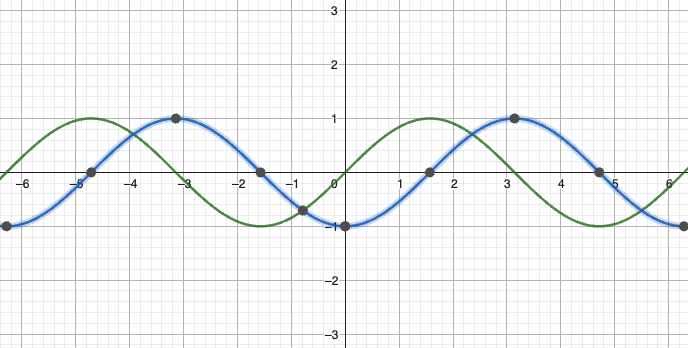
水平平移(相位移动)
数学表达式:
示例:原 波 峰 点 变 为
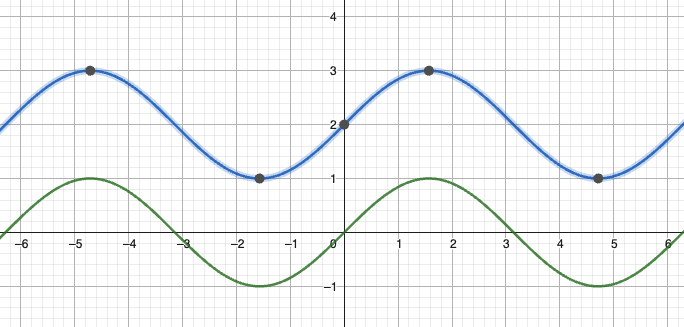
垂直平移
数学表达式:
示例:波 峰 值 , 波 谷 值
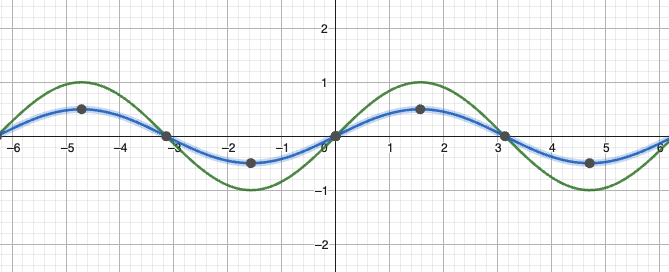
振幅调制
数学表达式:
示例:振 幅 , 波 形 倒 置
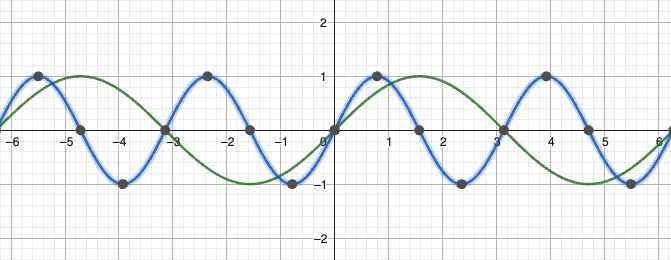
周期调整(频率变化)
数学表达式:
- 周期:
示例:( 原 周 期 的 )
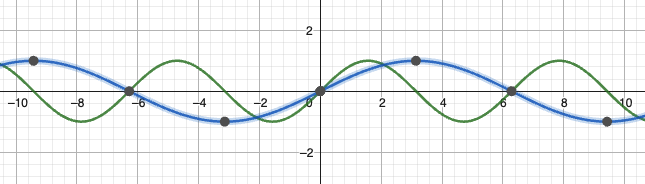
反射变换
关于
表达式:所 有 纵 坐 标 取 反 
示例:
关于
表达式:等 价 于 
示例:
复合变换示例
示例函数:
- 振幅:
- 周期:
- 相位移动:
- 垂直平移:上移
最终效果:
- 起点从
- 最大值点:
- 最小值点:
- Title: 三角函数的图像与特性
- Author: Neurocoda
- Created at : 2025-02-28 15:25:06
- Updated at : 2025-02-28 15:25:06
- Link: https://neurocoda.com/p/755aafe7.html
- License: This work is licensed under CC BY-ND 4.0.
Comments