导数本质探秘
导数标记
拉格朗日(Lagrange)记法
采用函数符号加撇号的形式表示导数。若
特点:
- 直接关联函数名称,便于理解函数与导数的对应关系
- 高阶导数通过撇号数量表示:二阶导数为
,三阶导数为
示例:的导数为:
适用场景: - 显式函数表达式(如
) - 理论证明与公式推导
莱布尼兹(Leibniz)记法
使用微分符号比表示导数。若
特点:
- 直观展现导数是微分之比的极限过程
- 高阶导数通过指数标记:二阶导数为
链式法则示例:
设
适用场景: - 隐函数方程(如
- 多变量微积分与物理方程
牛顿(Newton)记法
通过变量上方加点表示时间导数。若位移为
特点:
- 符号简洁,特别适合时间导数
- 超过三阶时采用多点记号(如
运动学示例:
自由落体运动速 度 加 速 度
适用场景: - 经典力学与动力学问题
- 微分方程组(如振动系统
比较与选用原则
| 记法类型 | 优势 | 局限性 |
|---|---|---|
| 拉格朗日 | 函数关系清晰 | 高阶导数符号冗长 |
| 莱布尼兹 | 直观反映微分本质 | 需注意非分数性质 |
| 牛顿 | 时间导数表达高效 | 仅适用于单变量时间函数 |
例如在热传导方程中,混合使用不同记法更高效:
定义
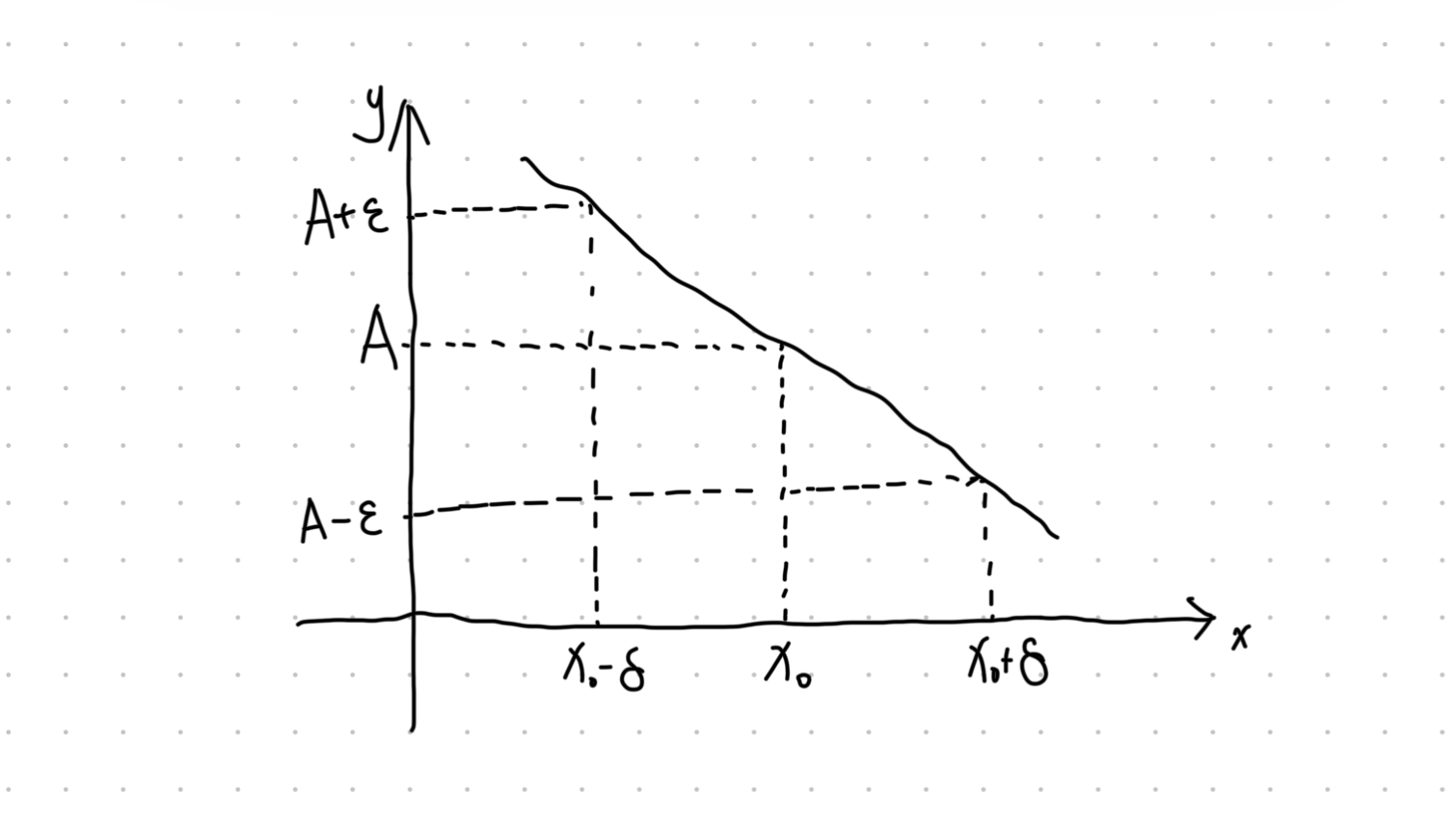
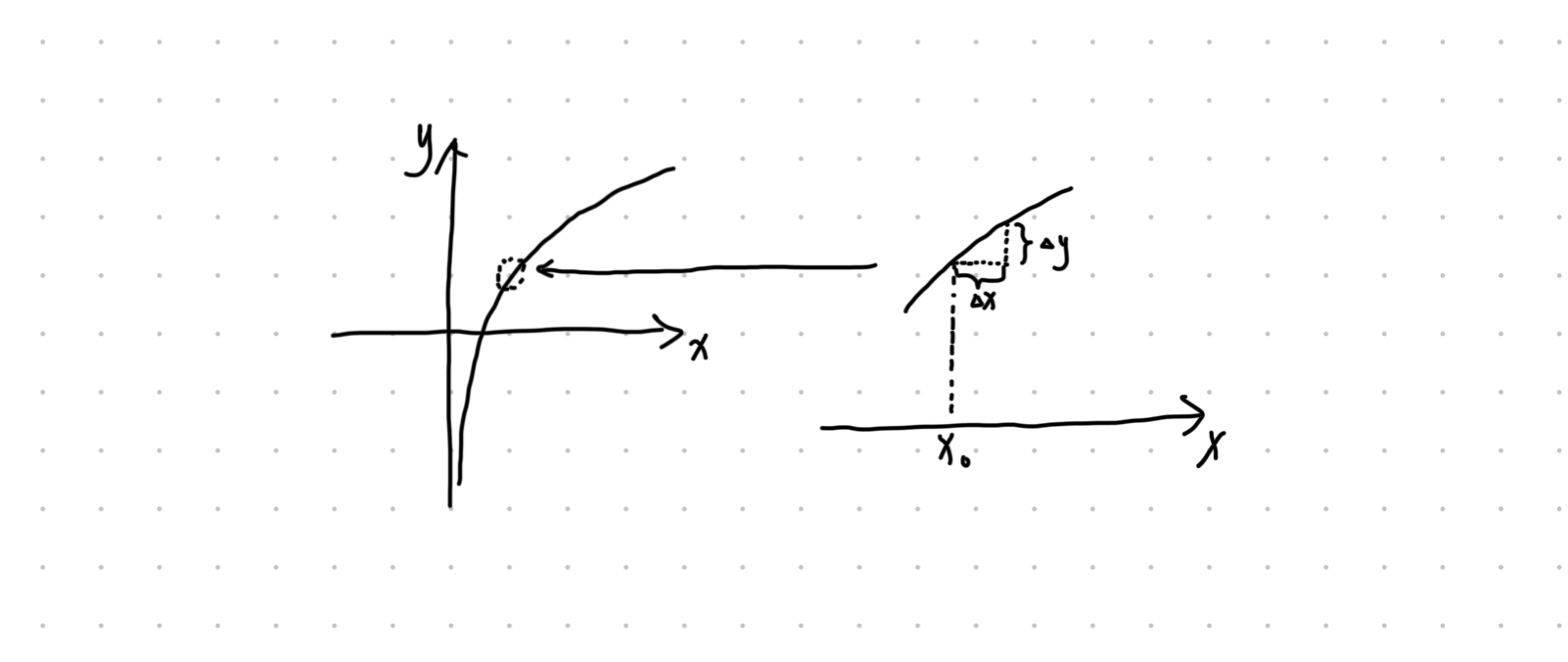
函数的导数定义为自变量增量趋近于零时,函数增量与自变量增量比值的极限。数学表达式为:
当极限存在时,称函数
从本质上说,导数的定义就是一个极限问题
通过定义式可以看出导数是通过 函数值变化量 与 自变量变化量 的比值来研究变化快慢的趋势的。
「从图像的角度来看,导数是函数
验证,函数

而这里的
如何更严谨地证明呢?
可以看到,在本图例中,当
是不是很眼熟?
运算法则
基本初等函数求导公式
| 函数类型 | 导数公式 |
|---|---|
| 常数函数 | |
| 幂函数 | |
| 指数函数 | |
| 自然指数函数 | |
| 对数函数 | |
| 自然对数函数 | |
| 正弦函数 | |
| 余弦函数 |
基本初等函数的求导公式当然可以通过导数的定义式计算出来的啦~
运算
加减法则
乘积法则
商法则
其中
都是基本初等函数
链式法则
对于复合函数,需要通过链式法则求导:
链式法则表明,复合函数的导数等于外层函数对内层函数的导数乘以内层函数的导数。直观理解就是,变化率的变化率等于各个变化率的乘积。
基本步骤:
- 识别复合函数中的外层函数和内层函数
- 求出外层函数的导数,保持内层函数不变
- 求出内层函数的导数
- 将两个导数相乘得到最终结果
示例 1:求
解析:令
- 外层函数导数:
- 内层函数导数:
- 应用链式法则:
示例 2:求
解析:令
- 外层函数导数:
- 内层函数导数:
- 应用链式法则:
示例 3:求
解析:令
- 外层函数导数:
- 内层函数导数:
- 应用链式法则:
多重复合函数的链式法则
对于多层嵌套的复合函数,可以连续应用链式法则:
示例:求
解析:可以将其视为
- 令
- 外层函数导数:
- 内层函数导数:
- 应用链式法则:
性质
可导条件
对于函数
$$
\begin{align}
\lim_{\Delta x \to 0^+} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} & = f’{+}(x_0) \
\lim{\Delta x \to 0^-} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} & = f’_{-}(x_0)
\end{align}
$$
其中,$f’{+}(x_0)
f’{+}(x_0) = f’{-}(x_0)
$$
则
可导与连续的关系
通过上述描述,很容易会想将可导性与连续性进行对比。这两个性质的定义的描述很相似不是吗?
连续性
若函数在 处连续,则有:
可导性
若函数在 处可导,则有:
$$f’(x) = f’{+}(x_0) = f’{-}(x_0)$$
在 超实数系视角下的函数极限 这篇文章中我们已经提到,以超实数的视角可以更好地理解函数极限。同样的,我们也可以更好地理解可导性。
这里我们先补充一下连续性:
函数
即以
而连续区间由实数构成,但这些实数在超实数模型中伴随着无限邻近的超实数。连续性在超实数视角下表现为无限小扰动下的函数值稳定性,而非空间的 「无缝连接」 。
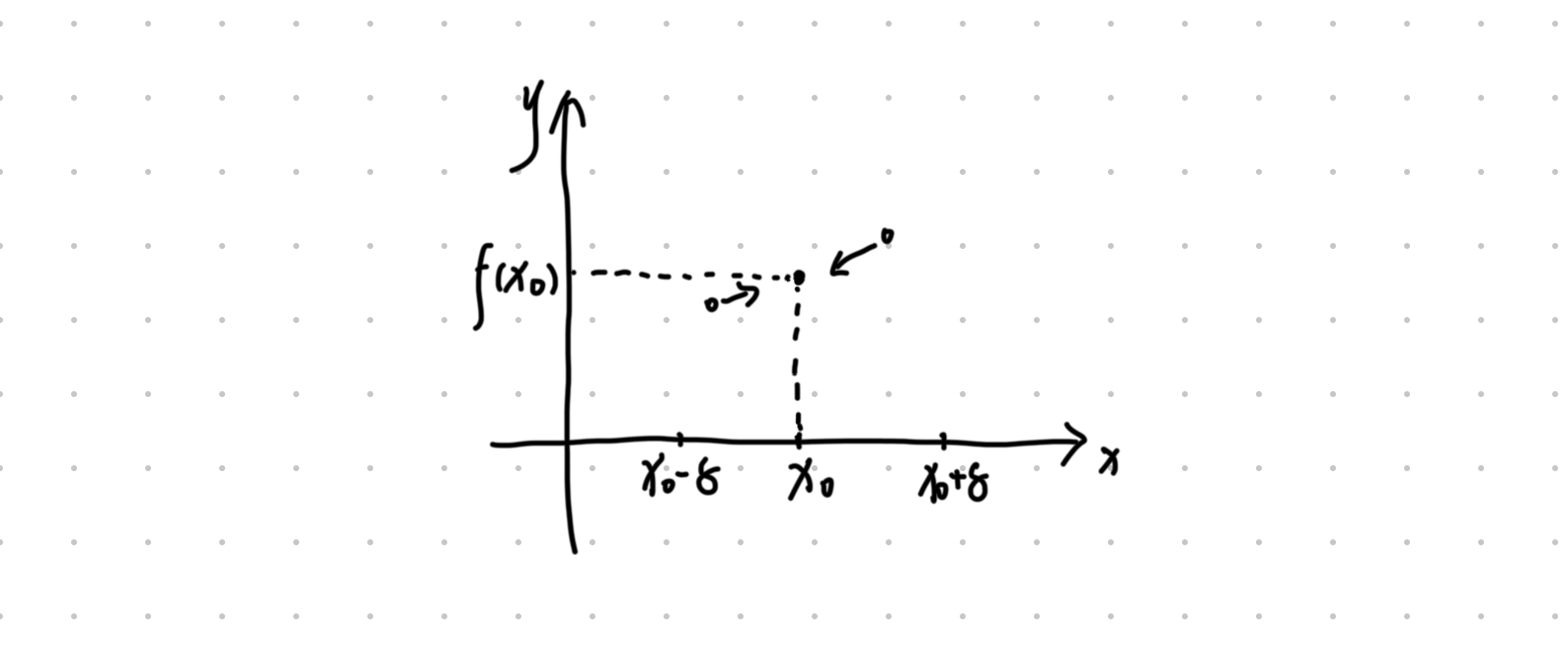
很明显,函数连续的定义:
好,我们继续看函数的可导性吧。
导数的定义:
当且仅当该极限有意义时,称函数可导。即:
对于
函数在
而可导性要求的条件相比连续性更多、更苛刻:
对于
那么可导性要求的条件同样更多、更苛刻:
那么可以得到结论:
原函数与其绝对值函数的连续、可导性分析
连续性
假设有原函数
对于
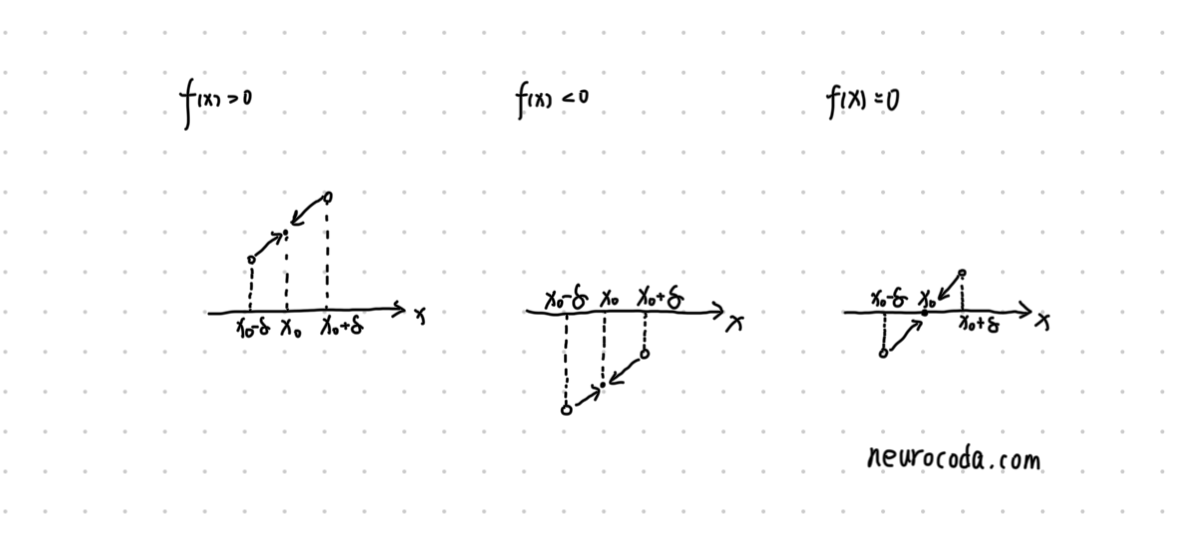
对于
显然,只要
那么
结论:
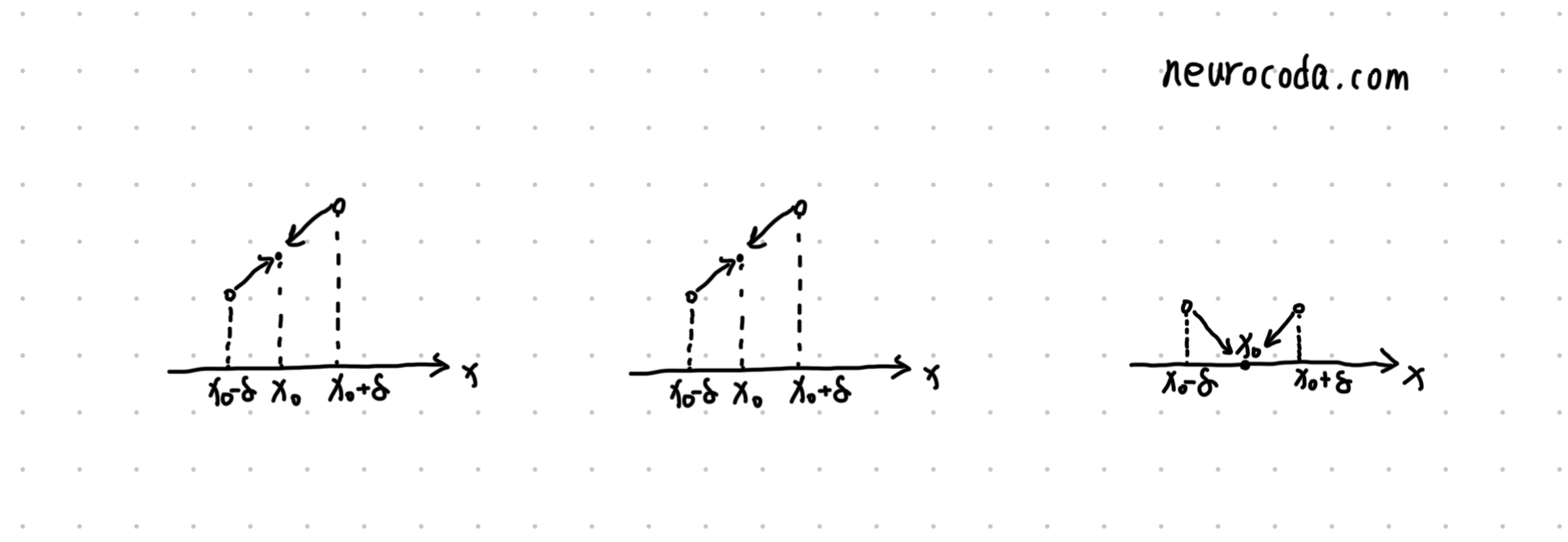
可导性
对于

对于

对于可导性,我们刚才已经说过了,可导性的要求比连续性更高,还需要
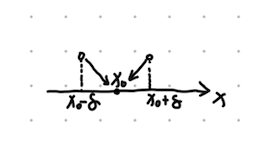
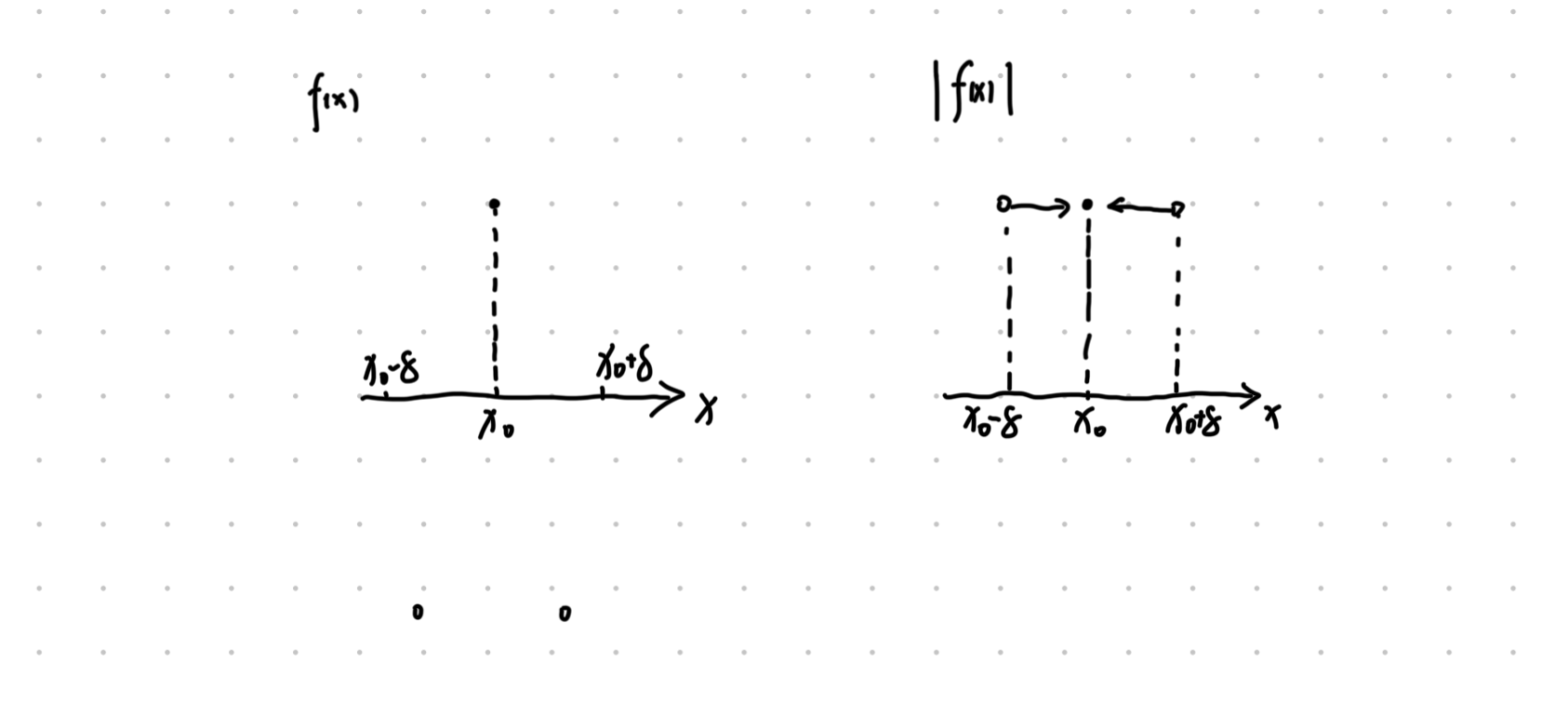
这个情况虽然满足连续性,但是不满足 $f’(x) = f’{+}(x_0) = f’{-}(x_0)
时候 图像与 轴重叠,
而必要性在上面连续性的证明中已经描述了,不再赘述。
可以归纳为:
导函数与原函数之间的奇偶性关系
这里先给出结论:
证明:
而
- Title: 导数本质探秘
- Author: Neurocoda
- Created at : 2025-03-11 14:58:21
- Updated at : 2025-03-11 14:58:21
- Link: https://neurocoda.com/p/7213ac96.html
- License: This work is licensed under CC BY-ND 4.0.