海涅定理的验证及练习

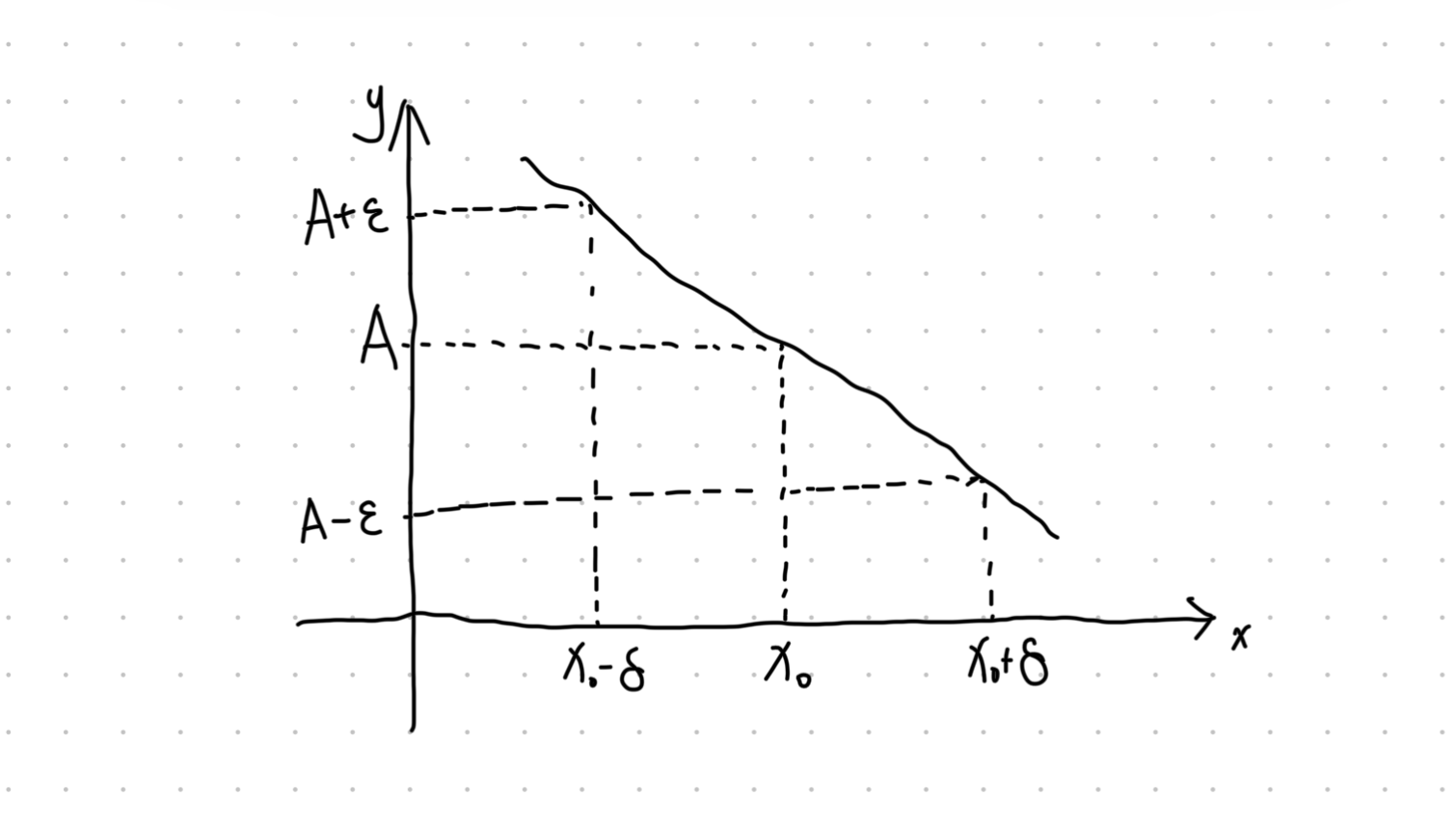
定义

设在内有定义，则存在对任何内的以为极限的数列，极限存在。

充分性证明

假设存在，需证对任意满足且的数列，有

证明步骤：

1. 根据函数极限定义：
   

2. 对上述，因，存在，使得当时：
   

3. 由函数极限定义可得：
   

4. 根据数列极限定义：
   

必要性证明

假设对任意满足且的数列，都有，需证

证明步骤（反证法）：

1. 假设，则存在，使得：
   

2. 构造特殊数列：取，对应存在满足：
   

3. 显然且，但数列不收敛于，与前提矛盾

练习

计算数列极限

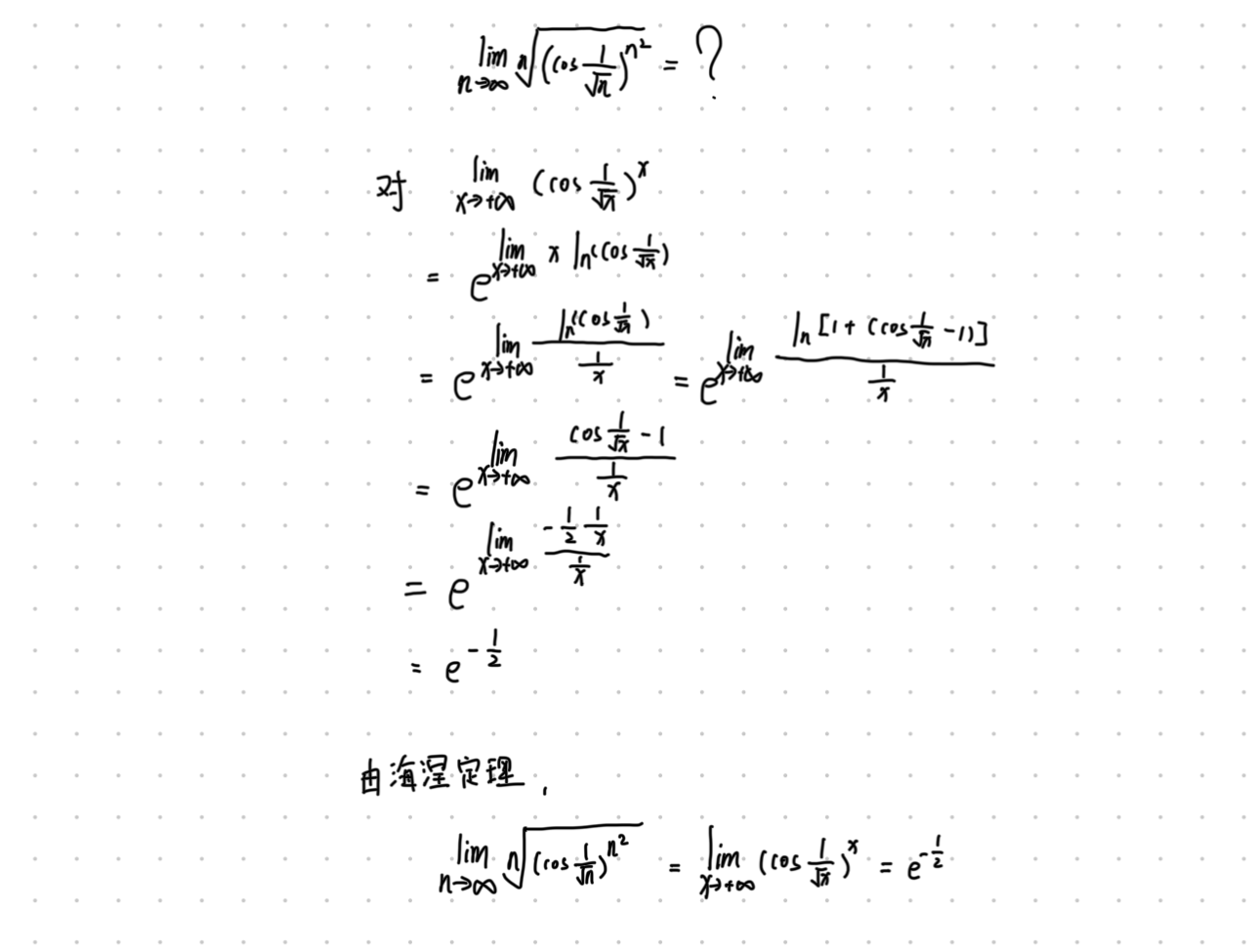
证明函数极限的不收敛

这里用到了数列收敛与子列收敛的关系（若数列收敛，则其任何子列也收敛），具体来说：

即：

• 若存在子列不收敛，则原数列不收敛
• 若存在两个子列收敛但收敛到不同的极限，则原数列不收敛（唯一性）