函数间断点的概念与分类

当函数在其定义域内某点不连续时，称该点为 间断点。根据极限存在性特征，间断点通常分为以下两类四型：

一类间断点

一类间断点指左右极限都存在但不满足连续条件的点，包括 可去间断点 和 跳跃间断点。

• 可去间断点
  判定条件：
  
  修复方法：
  重新定义后，函数在处连续。
  典型示例：
  

  

  在处：
  
  因此是可去间断点。

• 跳跃间断点
  判定条件：
  
  不可修复性：
  跳跃量无法通过重新定义消除。
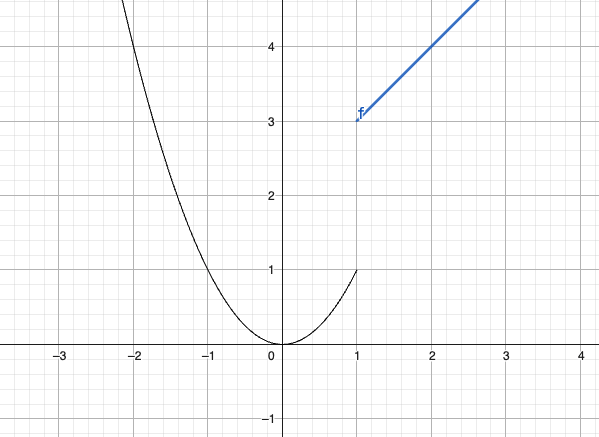
  分段函数示例：
  

  

  在处：
  
  两侧极限不相等，故为跳跃间断点。

二类间断点

二类间断点指至少有一侧极限不存在，或极限虽“存在”但趋于无穷的点，包括 无穷间断点 和 震荡间断点。

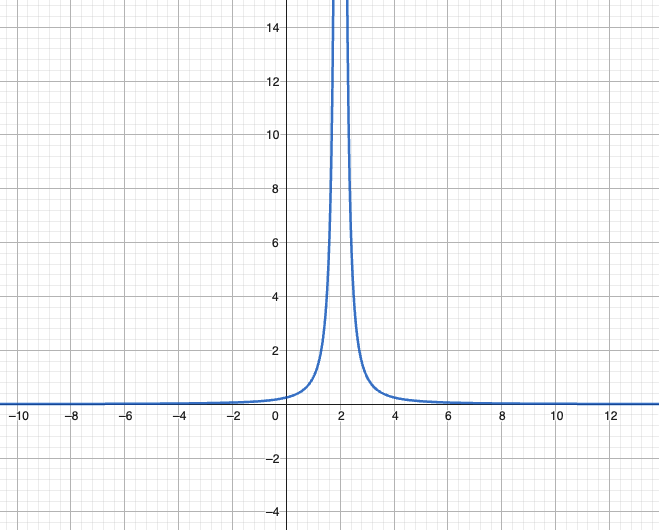
• 无穷间断点
  判定特征：
  
  此时函数图像在附近表现出竖直渐近线。
  典型示例：
  

  

  在处：
  

• 震荡间断点
  判定特征：
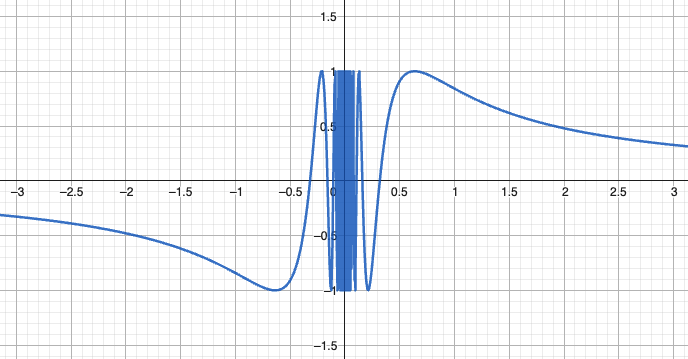
  在某点极限无穷次震荡于有限区间内，既不收敛到有限值，也不趋于无穷大。
  示例分析：
  

  

  当时，无界增大，使得在区间内无限振荡，左右极限都不存在，故处是震荡间断点。

关键位置与判断方法

在判断函数的间断点时，通常需要重点排查以下几类值，这些位置往往是间断点的潜在发生处。

• 定义域边界点
  例如的定义域是，在处函数仅有右侧定义，需要检查。若函数还有其它更小的区间，则需视具体情况判断单侧极限。

• 分段函数的连接点
  若函数以分段形式给出
  
  则必须检查处：
  、以及函数值三者之间的关系。

• 分母零点（有理函数）
  若，需要先解方程。对于满足的点，还要查看是否也为 0。

  • 若，通常是无穷间断点
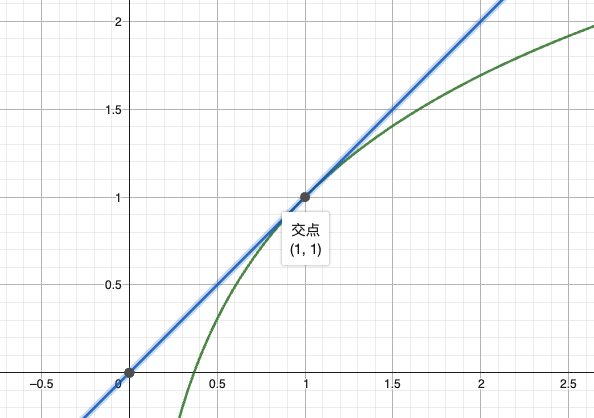
  • 若，需先约分再判断。例如
    
    在处约分后变为（），可知该点为可去间断点。

• 特殊函数结构点

函数类型	需检查的值	典型间断类型
对数函数	中	二类间断点
正切函数	中	无穷间断点
绝对值函数	在	通常连续（可导性变化）

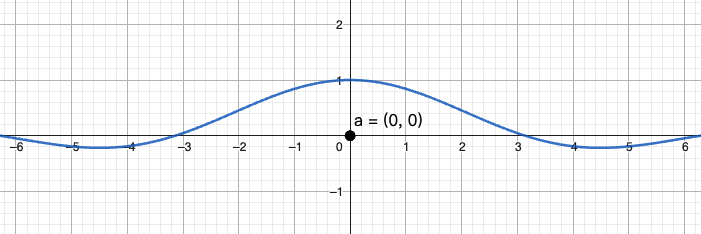
• 极限震荡点
  函数含、之类的“高频”震荡结构，往往在某些点（常见于）出现无限震荡，需要重点排查。

• 复合函数的连接点
  若外层函数对输入有额外限制，则需确定内层表达式满足该限制的范围。例如
  ，要保证（即），并在处检验单侧极限及函数值。

综合判断步骤

当确定了需要检查的候选点后，可以按照如下流程进行分析：

graph TD
    A[计算左极限] --> B[计算右极限]
    B --> C{极限存在?}
    C -->|是| D[一类间断分析]
    C -->|否| E[二类间断分析]

更详细的类型判别可以参考下述示意图：

graph TD

    A[待检查点 x_0] --> B{f x_0 是否已定义？}

    B -->|未定义| C[计算左右极限]
    B -->|已定义| C1[计算左右极限]

    C --> D{左右极限是否都存在？}
    C1 --> D{左右极限是否都存在？}

    D -->|否| E{可能是二类间断}
    E -->|若极限趋∞| F[无穷间断点]
    E -->|若极限震荡| G[震荡间断点]

    D -->|是| H{左右极限相等？}
    H -->|否| I[跳跃间断点]

    H -->|是| J{左右极限 = f x_0 ？}
    J -->|f x_0 未定义或不同| K[可去间断点]
    J -->|等于| L[连续点]

示例1：
分析

在处的间断情况：

• 由于无定义，首先判定为间断点。
• 计算单侧极限：
  
  左右极限不相等，属于跳跃间断点。

示例2：
判断

在处：

• 原函数未在明确定义，首先判定为间断。
• 然而通过夹逼定理：
  ，
  可得
  。
• 将补充定义为 0 后，可使其在处连续。故原点为可去间断点。

特殊情形处理

• 分段函数连接点
  要分别计算左极限和右极限，再与连接点的函数值进行比较。若三者相等则连续，否则为间断点。
  示例：
  
  在处：
  、、，
  三者相等，故连续。

• 导数存在性与间断
  若在可导，则必定在连续。
  但函数在某点不可导时，不一定间断，例如在处不可导，但函数仍连续。