三角不等式及其推广

三角不等式是数学中的一个基础而重要的概念，最初来源于几何学中三角形的基本性质，后来被推广到向量、绝对值、度量空间等多个领域。其核心思想是“两点之间直线最短”，这一原理在不同数学对象中呈现出多种形式。

几何形式

在平面几何中，三角不等式表现为 三角形任意两边之和大于第三边。对于三角形ABC，有：

同时可推导出 两边之差小于第三边：

向量形式

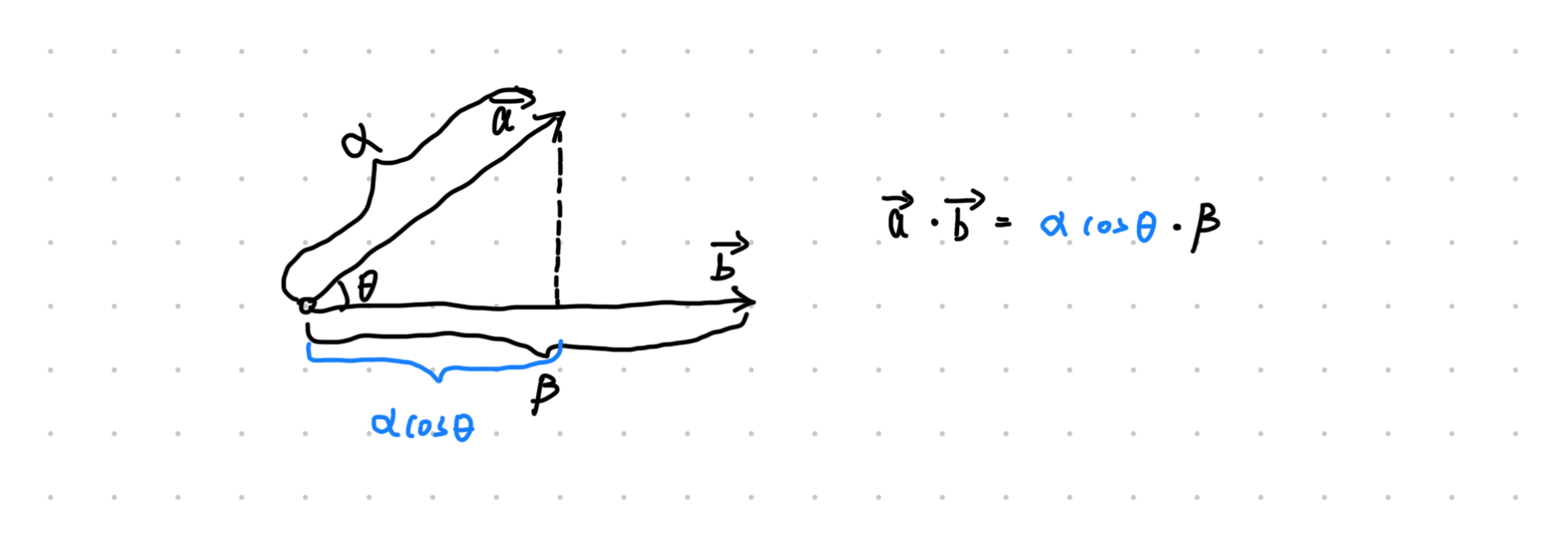
对于向量和，其模长满足：

几何解释：向量构成三角形的第三边，其长度受限于两边之和与差。

绝对值形式

实数和的绝对值满足：

加强形式：

证明：

1. 平方展开：。
2. 几何意义：实数在数轴上的加减对应向量的合成。

推广形式

• n个数推广：
  
• 度量空间：对任意三点，有：
  
  其中为距离函数，例如欧氏距离。