柯西不等式及其证明

简介

柯西不等式：

有取等条件：
当且仅当存在实数使得 每个与成比例，即对所有的满足：

此时不等式取等号。具体来说：

• 若存在非零常数使得（对所有成立），则左边达到最大值
• 当所有时，不等式两边均为，此时等号也成立（可视为时的特殊情况）

构造函数法证明

考虑实数的二次函数：

展开后得：

由于是非负二次函数（所以函数图像开口向上且与轴有至多一个交点），其判别式必须满足：

化简后即得柯西不等式：

几何视角证明

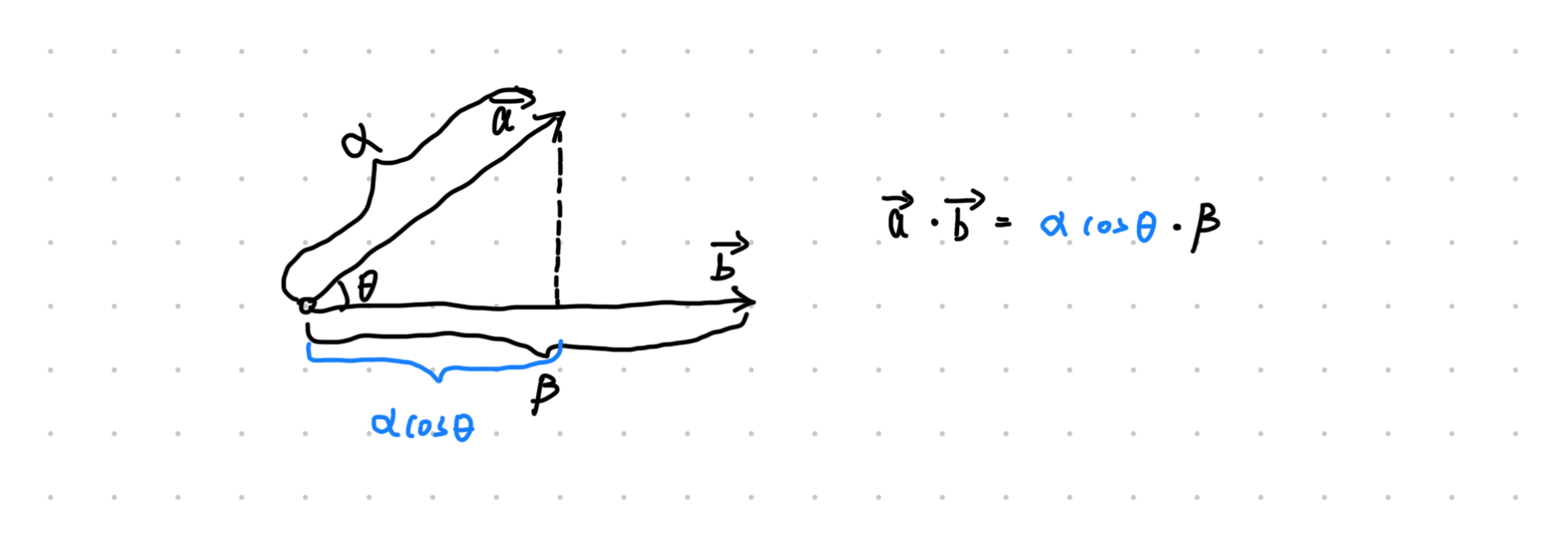
向量的内积（点乘）在几何上的核心意义是 量化两个向量在方向上的相似性与投影关系，具体可通过以下角度理解：

设向量和的夹角为，则内积，其几何意义如下：

投影长度
内积等于在方向上的 投影长度（）乘以的模长（），反之亦然。

• 若是单位向量（），则，直接表示在方向上的投影长度（含符号）。

方向相关性

• 当两向量 同向（），内积最大（）。
• 当两向量 垂直（），内积为。
• 当两向量 反向（），内积最小（）。

那么，从向量内积的角度，设，，则柯西不等式即：

当且仅当两向量 共线 时取等，即存在实数使得或。
因为当两向量共线时，内积达到极值，此时不等式取等号：

• 两向量 同向 时：
• 两向量 反向 时：
  那么