反函数的获取

反函数是函数关系的逆映射，其实质是将原函数的输出值唯一对应回输入值。理解反函数的关键在于把握定义域与值域的对应关系。

定义

设函数满足：

1. 单射性：若，则
2. 满射性：中每个元素都有原像

则存在唯一反函数，满足：

求解方法

求反函数的系统化流程：

1. 确认可逆性：通过水平线测试验证单射性（就是看函数图像的,是否一一对应），必要时限制原函数定义域
   （如限定）
2. 建立方程：设
3. 代数求逆：解方程得到
4. 规范形式：交换变量得，并标注定义域

典型案例分析

线性函数

原函数：

• 定义域：
• 值域：

求解过程：

反函数：

• 定义域：（继承原函数值域）
• 值域：（对应原函数定义域）

二次函数

原函数：（限定）

• 定义域：
• 值域：

求解过程：

反函数：

• 定义域：（与原函数值域一致）
• 值域：（对应原函数定义域）

指数函数

原函数：

• 定义域：
• 值域：

求解过程：

反函数：

• 定义域：（来自原函数值域）
• 值域：（对应原函数定义域）

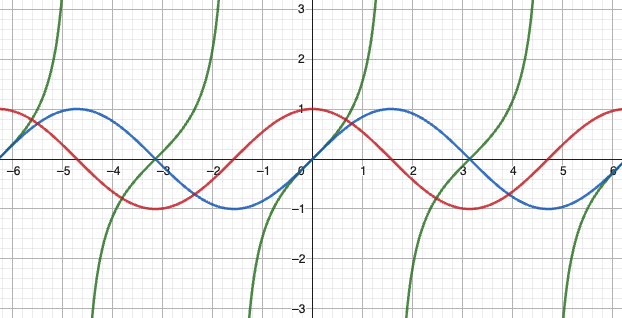
三角函数

原函数：（限定）

• 定义域：
• 值域：

反函数：

• 定义域：
• 值域：

核心规律

1. 定义域继承：反函数定义域严格等于原函数的值域
2. 值域对应：反函数值域必然匹配原函数的定义域限制
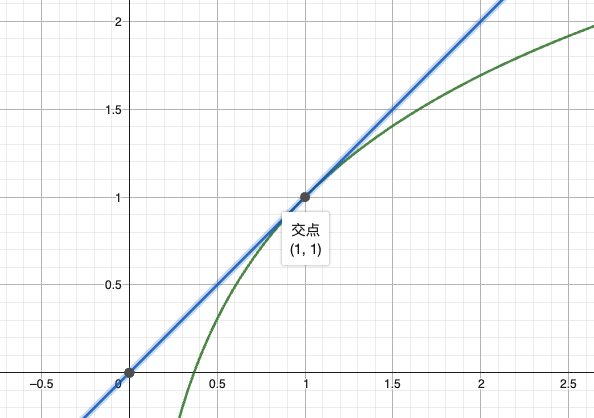
3. 图像对称：函数与其反函数图像关于直线对称