有下面常用的不等式链： 其中 证明几何均值 ≤ 算术均值证明：平方两边展开右边整理后得到： 调和均值 ≤ 几何均值证明：化简左边调和均值为平方两边得整理得 ，两边除以 后简化为：移项后得到 ，显然成立。 算术均值 ≤ 平方均值证明：平方两边得展开左边得整理后得到：最终简化为 ，显然成立。 拓展 适用范围：所有 ，且 。 我们依然是分步证明四个均值之间的不等式关系。 几何均值 ≤...
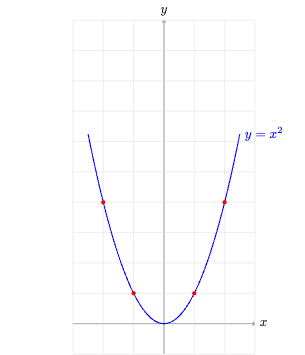
二次函数二次函数是形如 ，且 ， 是常数的多项式函数。其中 是自变量。 若令 ，则可以得到一个一元二次方程式。 函数图像通过代入不同的 值，我们可以得到一系列的点，连接这些点就形成了函数的图像： 具体的二次函数不等问题、区间最值问题，通过函数图像可以直观看出 一元二次方程一元二次方程式 是只含有一个未知数，并且未知数的最高次数是二次的多项式方程。 令 二次函数 即可得到标准的一...
数学中的数系体系经历了从简单到复杂的扩展过程，由于实际需求及运算的不封闭性，出现了数学问题，因而出现了数系的扩展。 graph TD %% === 主干数系演进 === A(自然数) -->|"减法不封闭"| B(整数) B -->|"除法不封闭"| C(有理数) C -->|"开方不封闭"| D(实数) D -->|"负数开方...
解析式 是用数学公式明确表达变量之间关系的方式，常见于函数、几何图形等数学对象的定义。 概念结构如下： flowchart TD 解析式 --> 代数式 解析式 --> 超越式 代数式 --> 有理式 代数式 --> 无理式 有理式 --> 整式 有理式 --> 分式 整式 --> 单项式...
二项式定理描述了如何展开形如 的二项式表达式。以下通过组合数学的视角，将抽象的代数展开转化为具体的计数问题，详细阐述其证明了定理。 二项式定理的表述对于任意非负整数 ，有：其中 是组合数（即 选 的方式数），定义为： 组合证明的核心思想核心思路：将 的展开过程视为从 个因子 中选择 或 的乘积组合，进而通过计数选择方式数来解释系数。 具体展开过程 乘积结构：将 视为 个...
数学归纳法简介数学归纳法是一种严谨的数学证明方法，通过有限步骤验证无限个命题的有效性。其核心思想类似于多米诺骨牌效应：验证首张牌会倒下（基例），并证明任意一张倒下必定导致下一张倒下（归纳步骤），从而保证所有骨牌依次倾倒。 基本步骤基例验证首先验证命题在初始自然数（通常为）时成立。例如证明前个自然数的立方和公式：当时，左边为，右边为，等式成立。 归纳假设假设命题对某个自然数成立，即： 归纳递推...
命题与条件的基本概念命题 定义：是一个陈述句，这个句子具有明确的真值，即该陈述句要么是真的，要么是假的。通常用小写字母（如 、）来表示简单命题。简单命题可以通过逻辑联结词组成复合命题。 例如： 雪是白色的。 这句话是陈述句 客观来说，该陈述句的描述是真的 条件 定义：条件特指命题之间的逻辑关系（如必要/充分条件），用于描述命题之间的蕴含性。 与命题的关系： 必要/充分条件是通过命...
前置准备：生成 SSH 密钥对 打开终端使用 Spotlight (⌘+Space) 搜索 “Terminal” 并打开 生成密钥对执行以下命令（替换your_email@example.com为你的邮箱）： 1ssh-keygen -t ed25519 -C "your_email@example.com" -f ~/.ssh/git_example 遇到提示时按 Enter 使用默认...
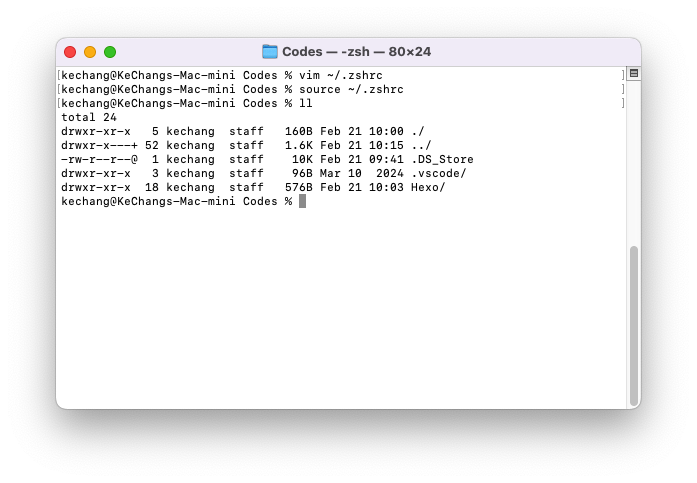
为什么需要 ll 命令？在 Ubuntu 系统中，ll 是 ls -alF 的默认别名，能直观展示： 文件权限 所有者信息 文件大小 隐藏文件而 Mac 终端默认未配置该别名，本文教你快速实现这个生产力工具。 三步配置教程步骤 1：定位配置文件 打开终端（Terminal） 输入以下命令编辑配置文件： 1vim ~/.zshrc 若使用 bash，请修改 ~/.bash_pro...
Hexo 是什么？ Hexo 是一个快速、简洁且高效的博客框架。 Hexo 使用 Markdown（或其他标记语言）解析文章，在几秒内，即可利用靓丽的主题生成静态网页。 本文对应的环境： 一台公网服务器 有 Git 平台托管 hexo 生成的站点（Github 或自建 Git 仓库） 本地能运行 Hexo 若你没有公网服务器，那么可以忽略本文 服务器配置 部分，转而采用类似 Github...
