基本替换公式当 时,有以下常用等价无穷小关系: 加减法替换规则加减运算中不可直接单独替换,但满足以下条件时可替换: 分子/分母整体代换时 高阶无穷小项可忽略时 示例: 原式 用泰勒展开 ,得极限值 乘除法替换规则乘除运算可直接替换: 特殊结构处理:对于复合指数形式 ,先取对数处理: 高阶无穷小替换当需要更高精度时,可使用泰勒展开: 应...
反函数是函数关系的逆映射,其实质是将原函数的输出值唯一对应回输入值。理解反函数的关键在于把握定义域与值域的对应关系。 定义设函数 满足: 单射性:若 ,则 满射性: 中每个元素都有原像 则存在唯一反函数 ,满足:且 求解方法求反函数的系统化流程: 确认可逆性:通过水平线测试验证单射性(就是看函数图像的 , 是否一一对应),必要时限制原函数定义域(如 限定 ) 建立方程:设 ...
函数奇偶性是分析函数对称性的重要工具,主要分为 偶函数 和 奇函数 两类。 定义偶函数满足 的函数,图像关于 轴对称。例如: 奇函数满足 的函数,图像关于 原点对称。例如: 唯一既是偶函数又是奇函数的函数是零函数 。 运算性质加减法规则 运算类型 结果性质 偶函数 + 偶函数 偶函数 奇函数 + 奇函数 奇函数 偶函数 ...
定义设有函数 在定义域 上有定义,若存在实数 ,使得对任意 都满足:则称 在 上为 有界函数。这个定义包含两个关键要素: 存在上界 和下界 对所有定义域内的自变量都成立 典型示例: 是全局有界函数() 在 上有界() 反例: 在 区间无界 常用性质加法:有界函数之和仍为有界函数 例: 仍满足 乘法:有界函数之积保持有界 例: 满足 除法:当分母不趋近零时...
要准确判断函数周期性需要系统分析函数结构并结合数学定义。我们首先从基础定义出发,再深入探讨复合函数情形,最后通过典型例题加深理解。 基本定义与判定方法函数 满足存在 非零实数 使得对于定义域内所有 都有:则称 为周期函数,最小的正周期称为 基本周期。 基本判定步骤: 观察函数类型:三角函数(如 、)、常数函数等具有明确周期性 验证定义关系式:通过解方程 寻找可能的周期 确定最小正...
数列的定义数列指按 确定顺序 排列的 无穷多个数 构成的集合,记作:或 项:数列中的每个数称为项(如为首项,为第n项) 通项公式:用关于n的表达式表示(如) 主要数列类型等差数列 定义:相邻项差恒为定值为公差 通项公式: 求和公式: 等比数列 定义:相邻项比值恒为定值为公比 通项公式: 求和公式: 常用解题方法错位相消法适用于 等差数列与等比数列乘积型求和,操作步骤: 写出原式 (...
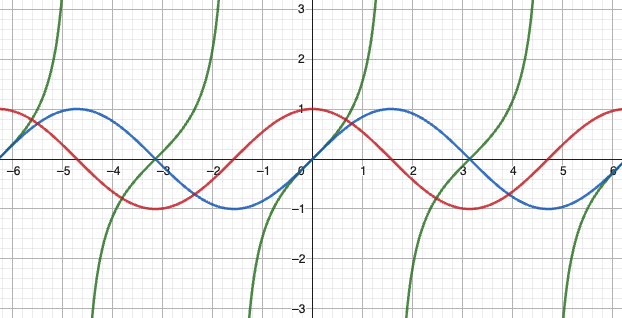
三角函数标准形式对边斜边邻边斜边 基本特性正弦函数 周期: 对称性:奇函数 极值点: 零点: 余弦函数 周期: 对称性:偶函数 极值点: 零点: 正切函数 周期: 渐近线: 值域: 特殊点:过原点,周期中心对称 核心性质导数与积分 函数 导数 积分 重要恒等式毕达哥拉斯恒等: 和角公式: 函数对比分析 特性 正弦函数 余...
在求解某些同时含有 和 的函数方程时,直接求解往往困难。此时可采用“倒代换法”:将自变量 替换为 ,得到新方程后与原方程联立消元,最终解出 的显式形式。 原理与思路设原方程为其中 为常数, 为待求函数。将 替换为 ,得到新方程:联立两方程消去 或 ,即可解出目标函数。 正确性证明可逆性说明 定义域限制:方程涉及 ,故仅当 时有意义。 双射变换:映射 在非零实数域上是双射...
算术平均数最常见,也是最好理解一种平均数。 几何平均数几何平均数被称为“几何”源于其在几何学中的直观解释和应用场景。几何平均数定义为n个正数乘积的 n 次方根,例如两个数 a 和 b 的几何平均数为。这种命名与古希腊数学家通过几何图形理解平均数的历史密切相关。在 的情况下可以理解为计算某个矩形面积对应同面积的正方形的边长, 的时候可以理解为计算同体积的正方体的边长,再推广就是多维物体对应...
三角不等式是数学中的一个基础而重要的概念,最初来源于几何学中三角形的基本性质,后来被推广到向量、绝对值、度量空间等多个领域。其核心思想是“两点之间直线最短”,这一原理在不同数学对象中呈现出多种形式。 几何形式在平面几何中,三角不等式表现为 三角形任意两边之和大于第三边。对于三角形ABC,有:同时可推导出 两边之差小于第三边: 向量形式对于向量 和 ,其模长满足:几何解释:向量 构成三角形...