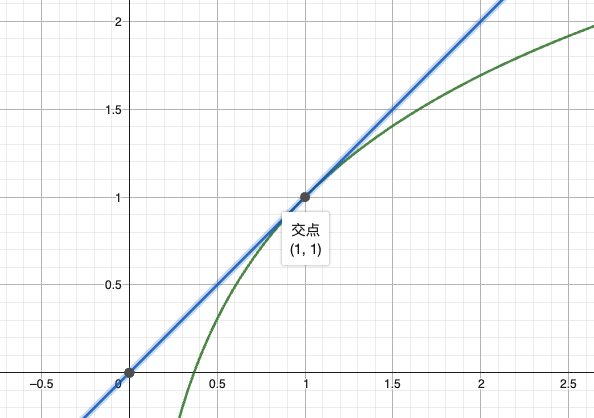
单项式与多项式的全局连续性单项式（如 ）和多项式（如 ）的连续性具有一个鲜明的特征：它们在 整个实数域上连续。这一性质源于： 基本构成单元的连续性：幂函数 和常数函数均在其定义域内连续； 运算封闭性：连续函数的加法、乘法保持连续性。例如，二次多项式 在任意区间 内： 对任意内点 ，满足 ； 闭区间端点满足单侧极限：关键结论：无需单独验证多项式和单项式在具体区间的连续性，其在整个定...
本文以函数 为例，详细讲解如何利用 泰勒级数法 和 莱布尼兹公式法 计算 （），并分析两种方法的等价性。 题目设 ，则当 时， 泰勒级数法核心思想将函数展开为泰勒级数，通过幂级数的系数直接读出高阶导数值。 具体步骤 展开 已知 在 内的泰勒展开为： 构造 的级数形式将 与上述级数相乘：通过变量替换 （即 ），级数改写为： 提取 项的系数当 时， 项的系数为 。根据泰...
导数标记拉格朗日（Lagrange）记法采用函数符号加撇号的形式表示导数。若 ，则： 或 特点： 直接关联函数名称，便于理解函数与导数的对应关系 高阶导数通过撇号数量表示：二阶导数为 ，三阶导数为 示例： 的导数为：适用场景： 显式函数表达式（如 ） 理论证明与公式推导 莱布尼兹（Leibniz）记法使用微分符号比表示导数。若 ，则： 或 特点： 直观展现导数是微分之比的极限过程 高阶...
定义设 在 内有定义，则 存在 对任何 内的以 为极限的数列 ，极限 存在。 充分性证明假设 存在，需证对任意满足 且 的数列 ，有 证明步骤： 根据函数极限定义：当时， 对上述 ，因 ，存在 ，使得当 时： 由函数极限定义可得： 根据数列极限定义： 必要性证明假设对任意满足 且 的数列 ，都有 ，需证 证明步骤（反证法）： 假设 ，则存在 ，...
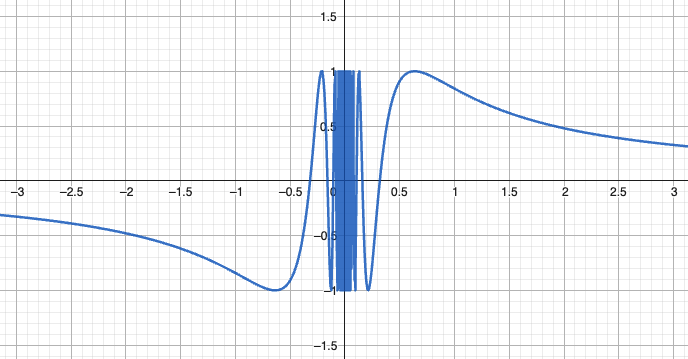
当函数在其定义域内某点不连续时，称该点为 间断点。根据极限存在性特征，间断点通常分为以下两类四型： 一类间断点一类间断点指左右极限都存在但不满足连续条件的点，包括 可去间断点 和 跳跃间断点。 可去间断点判定条件：或无定义修复方法：重新定义 后，函数在 处连续。典型示例： 在 处：但因此 是可去间断点。 跳跃间断点判定条件：且但不可修复性：跳跃量 无法通过重新定义 消除。分...
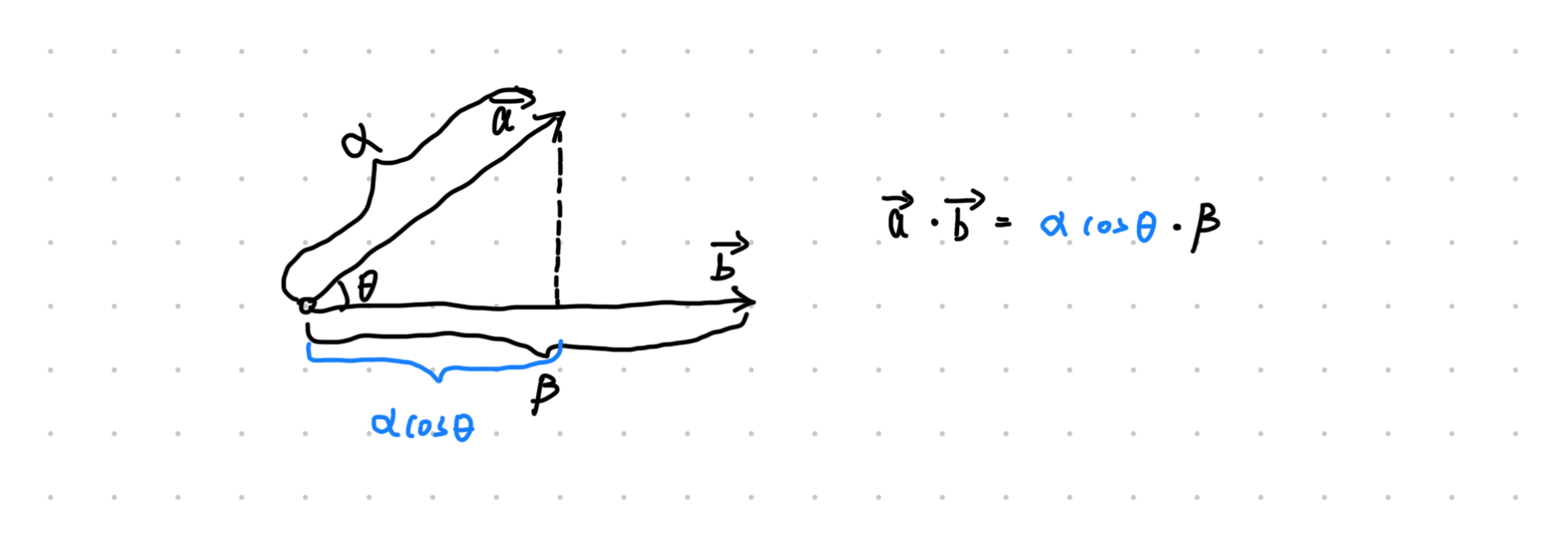
核心概念幅角合成法（又称 R 方法）是一种将形如的线性三角函数表达式转换为单一三角函数形式的方法。其核心思想是：通过构造合适的振幅 和相位角 ，可将上述表达式写为或。 步骤推导幅值计算幅值 的几何意义是向量 的模长，故有例如对于 ： 相位角确定根据目标形式（正弦或余弦）不同， 的计算方法略有差异，需结合 象限判断： 正弦形式：令利用和角公式展开：对比系数可得：因此 余弦形式：令...
简介柯西不等式：有取等条件：当且仅当存在实数 使得 每个 与 成比例，即对所有的 满足： 或 此时不等式取等号。具体来说： 若存在非零常数 使得 （对所有 成立），则左边 达到最大值 当所有 时，不等式两边均为 ，此时等号也成立（可视为 时的特殊情况） 构造函数法证明考虑实数 的二次函数：展开后得： 由于 是非负二次函数（所以函数图像开口向上且与 轴有至多一个交点...
泰勒展开是用多项式函数逼近复杂函数的重要工具，其核心思想是在某一点附近用无限阶可导函数的各阶导数信息构造多项式近似。 定义设函数 在 处 阶可导，则泰勒多项式为： 其中 指函数 的 阶导 当 时，若余项 ，则得到泰勒级数：特别地，当 时称为 麦克劳林展开。 常用展开以下是考研数学中常用到的泰勒展开式（麦克劳林展开式）: 仅在 时可用 三角函数指数函数二项式展开反三角...
基本替换公式当 时，有以下常用等价无穷小关系： 加减法替换规则加减运算中不可直接单独替换，但满足以下条件时可替换： 分子/分母整体代换时 高阶无穷小项可忽略时 示例： 原式 用泰勒展开 ，得极限值 乘除法替换规则乘除运算可直接替换： 特殊结构处理：对于复合指数形式 ，先取对数处理： 高阶无穷小替换当需要更高精度时，可使用泰勒展开： 应...
反函数是函数关系的逆映射，其实质是将原函数的输出值唯一对应回输入值。理解反函数的关键在于把握定义域与值域的对应关系。 定义设函数 满足： 单射性：若 ，则 满射性： 中每个元素都有原像 则存在唯一反函数 ，满足：且 求解方法求反函数的系统化流程： 确认可逆性：通过水平线测试验证单射性（就是看函数图像的 , 是否一一对应），必要时限制原函数定义域（如 限定 ） 建立方程：设 ...
